题目内容
一个圆的半径为3cm,圆外一点到圆心距离为6cm,则这点到圆的切点长为 cm; 这点与切点、圆心构成的三角形的最小锐角是 °.
考点:切线的性质
专题:
分析:运用切线的性质,结合直角三角形的边角关系、勾股定理等知识即可解决问题.
解答: 解:如图,∵AB为⊙O的切线,
解:如图,∵AB为⊙O的切线,
∴OB⊥AB;而OB=3,AO=6,
∴∠A=30°,∠B=60°;
由勾股定理得:AB2=OA2-OB2
=36-9=27,
∴AB=3
(cm),
∴答案为3
cm,30.
 解:如图,∵AB为⊙O的切线,
解:如图,∵AB为⊙O的切线,∴OB⊥AB;而OB=3,AO=6,
∴∠A=30°,∠B=60°;
由勾股定理得:AB2=OA2-OB2
=36-9=27,
∴AB=3
| 3 |
∴答案为3
| 3 |
点评:该题主要考查了切线的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对分析问题解决问题的能力提出了一定的要求.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
4°32′35″×6的结果为( )
| A、28°27′30″ |
| B、27°15′30″ |
| C、24°200′ |
| D、24°32′35″ |
 在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求
在正方形ABCD中,P是AB中点,PQ⊥AC,垂足为Q,求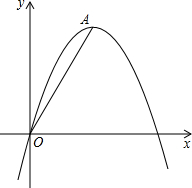 已知:如图,抛物线的解析式为y=-x2+4x.点A为顶点,连结OA,点B是抛物线上另一点.若△AOB是以OA为直角边的直角三角形,求点B的坐标.
已知:如图,抛物线的解析式为y=-x2+4x.点A为顶点,连结OA,点B是抛物线上另一点.若△AOB是以OA为直角边的直角三角形,求点B的坐标. 如图,△ABC中,AB=AC=5,AB的垂直平分线EF交AB、AC于E、F,若△BCF的周长为8,则BC的长为
如图,△ABC中,AB=AC=5,AB的垂直平分线EF交AB、AC于E、F,若△BCF的周长为8,则BC的长为