题目内容
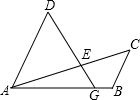 如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E.
如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E.(1)作出∠ABC的平分线BF,交AC于点F;(尺规作图,保留作图痕迹,不写作法与证明)
(2)试猜想DE与BF的数量关系,并加以证明.
考点:作图—复杂作图
专题:
分析:(1)以点B为圆心,以适当长为半径画弧,交边BA、BC于两点,再以这两点为圆心,适当长为半径画弧,在∠ABC内部交于点F,连接BF,则射线BF即为所求;
(2)易得,∠DAC=∠C,∠D=∠FBC,进而得出△ADE∽△CBF,进而得出DE与BF的数量关系.
(2)易得,∠DAC=∠C,∠D=∠FBC,进而得出△ADE∽△CBF,进而得出DE与BF的数量关系.
解答: (1)解:以B为圆心、适当长为半径画弧,交AB、BC于M、N两点,分别以M、N为圆心、大于
(1)解:以B为圆心、适当长为半径画弧,交AB、BC于M、N两点,分别以M、N为圆心、大于
MN长为半径画弧,两弧相交于点P,过B、P作射线BF交AC于F.
(2)证明:∵AD∥BC,∴∠DAC=∠C.
∵BF平分∠ABC,∴∠ABC=2∠FBC,
又∵∠ABC=2∠ADG,∴∠D=∠FBC,
∴△ADE∽△CBF,
∴
=
=2,
∴DE=2BF.
 (1)解:以B为圆心、适当长为半径画弧,交AB、BC于M、N两点,分别以M、N为圆心、大于
(1)解:以B为圆心、适当长为半径画弧,交AB、BC于M、N两点,分别以M、N为圆心、大于| 1 |
| 2 |
(2)证明:∵AD∥BC,∴∠DAC=∠C.
∵BF平分∠ABC,∴∠ABC=2∠FBC,
又∵∠ABC=2∠ADG,∴∠D=∠FBC,
∴△ADE∽△CBF,
∴
| AD |
| BC |
| DE |
| FB |
∴DE=2BF.
点评:本题主要考查了相似三角形的判定与性质和基本作图,学生应熟练掌握证明三角形相似的几个判定定理及其性质.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、x+y=xy |
| B、x2•x3=x5 |
| C、x2+2xy-y2=(x-y)2 |
| D、3x-2x=1 |
 如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.
如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上. 在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推….我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、纵坐标之和为l3,l3=18;按照这样的规律,
在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推….我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、纵坐标之和为l3,l3=18;按照这样的规律, 如图,在菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上.
如图,在菱形ABCD中,∠B=60°,点E、F分别在边BC、CD上.