题目内容
已知直线y=kx-3k+2与双曲线y=
x(x>0)交于点A,与x轴交于点B,若S△ABO=2,则k值为 .
| 2 |
| 3 |
考点:反比例函数与一次函数的交点问题
专题:压轴题
分析:分别求得直线y=kx-3k+2与双曲线y=
x(x>0)的交点A的坐标,与x轴的交点B的坐标,再根据S△ABO=2,可得关于k的方程,从而求得k的值.
| 2 |
| 3 |
解答:解:∵直线y=kx-3k+2与双曲线y=
x(x>0)交于点A,
∴kx-3k+2=
x,
解得x=3,
y=
×3=2,
∵直线y=kx-3k+2与x轴交于点B,
∴kx-3k+2=0,
解得x=3-
,
∵S△ABO=2,
∴|3-
|×2÷2=2,
解得k1=2,k2=
(不合题意舍去).
故答案为:2.
| 2 |
| 3 |
∴kx-3k+2=
| 2 |
| 3 |
解得x=3,
y=
| 2 |
| 3 |
∵直线y=kx-3k+2与x轴交于点B,
∴kx-3k+2=0,
解得x=3-
| 2 |
| k |
∵S△ABO=2,
∴|3-
| 2 |
| k |
解得k1=2,k2=
| 2 |
| 5 |
故答案为:2.
点评:考查了反比例函数与一次函数的交点问题和三角形的面积计算,解题的关键是根据三角形的面积公式得到关于k的方程,解方程求得k的值.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
代数式
,-
x,
中是分式的有( )
| 1 |
| x |
| 3 |
| 2 |
| 4 |
| x-7 |
| A、1个 | B、2个 | C、3个 | D、0个 |
某小组的8名学生体育中考成绩分别为38,35,34,32,38,40,39,38,这组数据的众数和中位数分别为( )
| A、38,37.5 |
| B、37,37.5 |
| C、38,38 |
| D、38,37 |
不等式组
的解集,在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
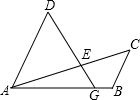 如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E.
如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E. 如图,△ABC内接于⊙O,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径
如图,△ABC内接于⊙O,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径