题目内容
 如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.
如图,⊙O是△ABC是的外接圆,BC为⊙O直径,作∠CAD=∠B,且点D在BC的延长线上.(1)求证:直线AD是⊙O的切线;
(2)若sin∠CAD=
| ||
| 4 |
考点:切线的判定,解直角三角形
专题:计算题
分析:(1)连结OA,根据圆周角定理的推论得到∠BAC=90°,由∠CAD=∠B易得∠BAO=∠CAD,则∠CAD+∠CAO=90°,于是OA⊥AD,然后根据切线的判定方法即可得到直线AD是⊙O的切线;
(2)在Rt△ABC中,由sinB=sin∠CAD=
,根据正弦的定义可计算出AC=2
,再根据勾股定理可计算出AB=2
,利用△DAC∽△DBA得
=
=
=
,即AD=
CD,然后在Rt△OAD中,根据勾股定理可得到关于CD的方程,然后解方程得CD的长.
(2)在Rt△ABC中,由sinB=sin∠CAD=
| ||
| 4 |
| 2 |
| 14 |
| CD |
| AD |
| AC |
| AB |
2
| ||
2
|
| 1 | ||
|
| 7 |
解答:(1)证明:连结OA,如图,
∵BC为⊙O直径,
∴∠BAC=90°,即∠BAO+∠CAO=90°,
∵OA=OB,
∴∠B=∠BAO,
而∠CAD=∠B,
∴∠BAO=∠CAD,
∴∠CAD+∠CAO=90°,即∠OAD=90°,
∴OA⊥AD,
∴直线AD是⊙O的切线;
(2)在Rt△ABC中,sinB=sin∠CAD=
,
而sinB=
,BC=8,
∴AC=2
,
∴AB=
=2
,
∵∠CAD=∠B,
∴△DAC∽△DBA,
∴
=
=
=
,即AD=
CD,
在Rt△OAD中,OA=OC=4,
∵OA2+AD2=OD2,
∴42+(
CD)2=(4+CD)2,
∴CD=
.

∵BC为⊙O直径,
∴∠BAC=90°,即∠BAO+∠CAO=90°,
∵OA=OB,
∴∠B=∠BAO,
而∠CAD=∠B,
∴∠BAO=∠CAD,
∴∠CAD+∠CAO=90°,即∠OAD=90°,
∴OA⊥AD,
∴直线AD是⊙O的切线;
(2)在Rt△ABC中,sinB=sin∠CAD=
| ||
| 4 |
而sinB=
| AC |
| BC |
∴AC=2
| 2 |
∴AB=
| BC2-AC2 |
| 14 |
∵∠CAD=∠B,
∴△DAC∽△DBA,
∴
| CD |
| AD |
| AC |
| AB |
2
| ||
2
|
| 1 | ||
|
| 7 |
在Rt△OAD中,OA=OC=4,
∵OA2+AD2=OD2,
∴42+(
| 7 |
∴CD=
| 4 |
| 3 |
点评:本题考查了切线的判定:过半径的外端点与半径垂直的直线是圆的切线.也考查了勾股定理、相似三角形的判定与性质以及圆周角定理的推论.

练习册系列答案
相关题目
 如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,则下列结论正确的是( )
如图,抛物线y=ax2+bx+c(a≠0)的对称轴x=-2,则下列结论正确的是( )| A、abc<0 |
| B、4a+b=0 |
| C、9a-3b+c<0 |
| D、3a+c>0 |
若⊙O1,⊙O2的半径分别是r1=5,r2=3,圆心距d=8,则这两个圆的位置关系是( )
| A、内切 | B、相交 | C、外切 | D、外离 |
某小组的8名学生体育中考成绩分别为38,35,34,32,38,40,39,38,这组数据的众数和中位数分别为( )
| A、38,37.5 |
| B、37,37.5 |
| C、38,38 |
| D、38,37 |
 如图,已知AD∥BC,DB平分∠ADE,∠CED=62°,则∠B的度数为( )
如图,已知AD∥BC,DB平分∠ADE,∠CED=62°,则∠B的度数为( )| A、31° | B、62° |
| C、28° | D、18° |
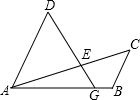 如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E.
如图,G是线段AB上的一点,AD∥BC且AD=2BC,∠ABC=2∠ADG,AC与DG相交于点E.