题目内容
16.某校在“校艺术节”期间,举办了A演讲,B唱歌,C书法,D绘画共四个项目的比赛,要求每位同学必须参加且限报一项,以九年(一)班为样本进行统计,并将统计结果绘制如下尚不完整的条形和扇形统计图,请根据统计图解答下列问题:(1)在扇形统计图中,D项的百分率是多少?
(2)在扇形统计图中,C项的圆心角的度数是多少?
(3)请补充完整条形统计图;
(4)若该校九年级有500名学生,那么九年级参加演讲和唱歌比赛的学生共有多少人?
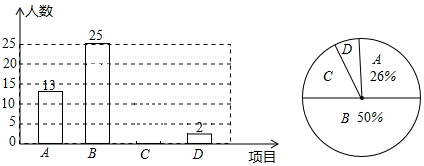
分析 (1)根据A的人数及其百分比得出总人数,绘画人数除50即可.
(2)两图结合,按频数和频率的关系知c=20%,由此即可求出相应圆心角的度数;
(3)总人数减去其余各组人数得出C组人数,即可补全图形;
(3)利用样本估计总体即可.
解答 解:(1)∵参加比赛的总人数为13÷26%=50人,
∴参加绘画比赛的学生人数占全班总人数的百分比是$\frac{2}{50}$×100%=4%;
(2)根据题意得:
360°×(1-26%-50%-4%)=72°.
则参加书法比赛的C项所在的扇形圆心角的度数是72°.
(3)参加书法的人数为50-(13+25+2)=10,补全图象如下:
(4)∵500×(50%+26%)=380,
∴九年级参加演讲和唱歌比赛的学生约有380人.
点评 本题主要考查条形统计图和扇形统计图,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
6.若|x-3|与|2y-3|互为相反数,则xy+x-y的值是( )
| A. | 6 | B. | -6 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
4.某天的最高气温是5℃,最低气温是-4℃,则这一天气温的温差是( )
| A. | 1℃ | B. | -1℃ | C. | 9℃ | D. | -9℃ |
11.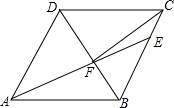 如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( )
 如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( )
如图,在菱形ABCD中,AB=6,∠DAB=60°,点E在BC边上,且CE=2,AE与BD交于点F,连接CF,则下列结论不正确的是( )| A. | △ABF≌△CBF | B. | △ADF∽△EBF | C. | tan∠EAB=$\frac{\sqrt{3}}{3}$ | D. | S△EAB=6$\sqrt{3}$ |
1.若代数式$\frac{\sqrt{x+1}}{x-2}$在实数范围内有意义,则实数x的取值范围是( )
| A. | x≥-1 | B. | x>2 | C. | x≠2 | D. | x≥-1且x≠2 |
5.某体校要从四名射击选手中选拔一名参加体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩及其方差s2如表所示,如果要选出一名成绩高,且发挥稳定的选手参赛,则应选择的选手是乙.
| 甲 | 乙 | 丙 | 丁 | |
| $\overline{x}$(环) | 8.4 | 8.6 | 8.6 | 7.6 |
| S2 | 0.74 | 0.56 | 0.94 | 1.92 |
6. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A-DME剪下围成一个圆锥,则圆锥的高为( )
如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A-DME剪下围成一个圆锥,则圆锥的高为( )
 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A-DME剪下围成一个圆锥,则圆锥的高为( )
如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A-DME剪下围成一个圆锥,则圆锥的高为( )| A. | 1 | B. | 4 | C. | $\sqrt{15}$ | D. | $\sqrt{17}$ |
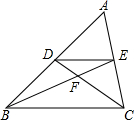 如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( )
如图,在任意△ABC中,DE∥BC,连接BE与CD相交于点F,则下列结论一定正确的有几个( )