题目内容
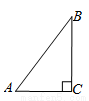
如图，△ABC中，AB=AC，D是BC中点，BE⊥AC于E．求证：△ACD∽△BCE．
证明见试题解析．
【解析】
试题分析：利用等腰三角形三线合一的性质，得到AD⊥BC，再证明两个三角形相似．
试题解析：∵AB=AC，D是BC中点，∴AD⊥BC，∴∠ADC=90°．∵BE⊥AC，∴∠BEC=90°．∴∠ADC=∠BEC．在△ACD和△BCE中，∵∠ACD=∠BCE，∠ADC=∠BEC，∴△ACD∽△BCE．
考点：1．相似三角形的判定；2．等腰三角形的性质．
练习册系列答案
口算题天天练系列答案
相关题目
，那么
=________________；
，E是AB的中点，tanD=2，CE=1，求sin∠ECB和AD的长．
B．
C．
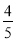D．
有两个不相等的实数根
，
．
，且
，求整数m的值．
，则
的值为（ ）
B．
C．
D．
，OC=3，那么⊙O的半径等于 ．
与y轴交于（0,3）点.
的根是多少？
？