题目内容
14.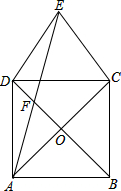 如图,四边形ABCD是正方形,对角线AC、BD相交于点O,△CDE是等边三角形,连接AE交BD于点F.求证:
如图,四边形ABCD是正方形,对角线AC、BD相交于点O,△CDE是等边三角形,连接AE交BD于点F.求证:(1)AF=2OF.
(2)FE=FB.
分析 (1)先根据正方形和等边三角形的性质证明△ADE是等腰三角形,求出∠DAE=∠DEA,再求出∠OAF=30°,在直角三角形OAF中即可得出结论;
(2)连接BE,证明∠FBE=∠AEB,即可得出结论.
解答 证明:(1)∵四边形ABCD是正方形,△CDE是等边三角形,
∴AD=CD,∠ADC=90°,DC=DE,∠CDE=∠DEC=60°,∠DAC=45°,AC⊥BD,
∴AD=DE,∠ADE=90°+60°=150°,∠AOD=90°, ∴∠DAE=∠DEA=$\frac{1}{2}$(180°-150°)=15°,∠OAF=45°-15°=30°,
∴∠DAE=∠DEA=$\frac{1}{2}$(180°-150°)=15°,∠OAF=45°-15°=30°,
∴AF=2OF;
(2)连接BE,如图所示:
由(1):∠DEA=15°,∠OAF=30°,
同理得:∠CEB=15°,∠FBE=30°,
∴∠AEB=60°-15°-15°=30°,
∴∠FBE=∠AEB,
∴FE=FB.
点评 本题考查了正方形的性质和等边三角形的性质、含30°角的直角三角形的性质以及等腰三角形的判定方法;根据正方形和等边三角形的性质弄清各个角之间的关系是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
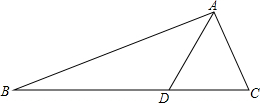 如图,在△ABC中,点D在BC上,BD=2DC,若AC=5cm,AD=6cm,CD=5cm.
如图,在△ABC中,点D在BC上,BD=2DC,若AC=5cm,AD=6cm,CD=5cm.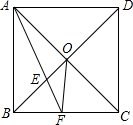 如图,已知正方形ABCD边长为2,AF平分∠BAC,求OF的长.
如图,已知正方形ABCD边长为2,AF平分∠BAC,求OF的长.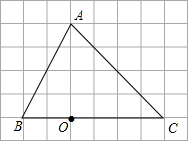 如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网络图中作△A′B′C′,使△A′B′C′和△ABC位似,且AB=2A′B′.
如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均为小正方形的顶点.以O为位似中心,在网络图中作△A′B′C′,使△A′B′C′和△ABC位似,且AB=2A′B′.