题目内容
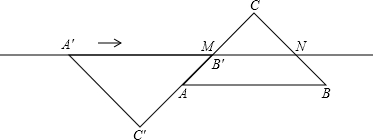
如图，直线l是等腰直角三角形EFG和正方形ABCD的对称轴，点G在AD边上，且F、A、B在同一直线上，若等腰直角三角形EFG沿直线l从左到右平移，当EF与CB重合时停止移动，移动过
程中△EFG与正方形ABCD重叠部分的面积（S）随平移距离（x）变化的图象大致是
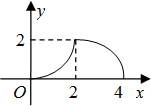
- A.
- B.
- C.
- D.
D
分析：本题是分段函数．分别把重合的三种情况作图，分别分析可知第一段和第三段是二次函数，第二段是平行与x轴的直线，从而判断函数图象．
解答：如下图：
①设直角三角形得与正方形重合部分的三角形的高是x，则底边为2x，那么其面积为y=x2；
②由图可知，重合部分是直角三角形，y是定值；
③重合部分是等腰梯形，结合①可知是S△EFG减去走出正方形的小直角三角形的面积，由①可知，③中的函数也是二次函数且S随T减小．
综上可知，该函数是分段函数，分为三段，第一段和第三段是二次函数两个开口不一样，第二段是平行与x轴的直线．
故选D．
①
②
③
点评：解决有关动点问题的函数图象类习题时，关键是要根据条件找到所给的两个变量之间的函数关系，在本题中只要根据题意得到重合面积大小变化的规律即可．
分析：本题是分段函数．分别把重合的三种情况作图，分别分析可知第一段和第三段是二次函数，第二段是平行与x轴的直线，从而判断函数图象．
解答：如下图：
①设直角三角形得与正方形重合部分的三角形的高是x，则底边为2x，那么其面积为y=x2；
②由图可知，重合部分是直角三角形，y是定值；
③重合部分是等腰梯形，结合①可知是S△EFG减去走出正方形的小直角三角形的面积，由①可知，③中的函数也是二次函数且S随T减小．
综上可知，该函数是分段函数，分为三段，第一段和第三段是二次函数两个开口不一样，第二段是平行与x轴的直线．
故选D．
①
②
③
点评：解决有关动点问题的函数图象类习题时，关键是要根据条件找到所给的两个变量之间的函数关系，在本题中只要根据题意得到重合面积大小变化的规律即可．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
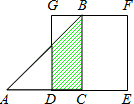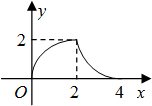
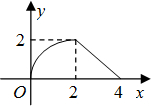
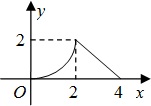
如图，等腰Rt△ABC（∠ACB=90°）的直角边与正方形DEFG的边长均为2，且AC与DE在同一直线上，开始时点C与点D重合，让△ABC沿这条直线向右平移，直到点A与点E重合为止．设CD的长为x，△ABC与正方形DEFG重合部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
如图，等腰直角三角形△ABC的直角边与正方形MNPQ的边长都为4cm，且在同一直线上，开始时A点与M点重合，让△ABC向右平移，直到点C与点N重合．设阴影部分面积为y（cm2），MA的长为x（cm），则y与x之间的函数关系的图象大致是（ ）