题目内容
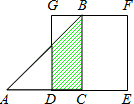 如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )
如图,等腰Rt△ABC(∠ACB=90°)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y,则y与x之间的函数关系的图象大致是( )A、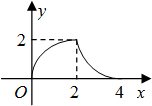 | B、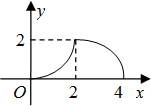 | C、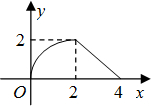 | D、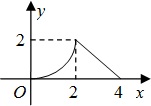 |
分析:此题可分为两段求解,即C从D点运动到E点和A从D点运动到E点,列出面积随动点变化的函数关系式即可.
解答:解:设CD的长为x,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为y∴
当C从D点运动到E点时,即0≤x≤2时,y=
×2×2-
(2-x)×(2-x)=-
x2+2x.
当A从D点运动到E点时,即2<x≤4时,y=
×[2-(x-2)]×[2-(x-2)]=
x2-4x+8
∴y与x之间的函数关系
由函数关系式可看出A中的函数图象与所求的分段函数对应.
故选A.
当C从D点运动到E点时,即0≤x≤2时,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当A从D点运动到E点时,即2<x≤4时,y=
| 1 |
| 2 |
| 1 |
| 2 |
∴y与x之间的函数关系
|
由函数关系式可看出A中的函数图象与所求的分段函数对应.
故选A.
点评:本题考查的动点变化过程中面积的变化关系,重点是列出函数关系式,但需注意自变量的取值范围.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
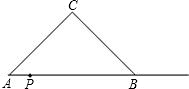 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.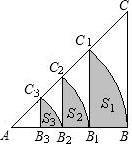 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=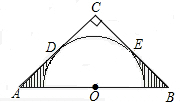 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)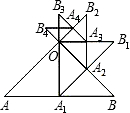 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是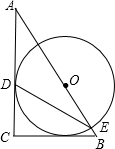 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.