题目内容
19.已知$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,根据你发现的规律,回答下列问题.(1)写出第n个式子;
(2)利用规律计算:$\frac{1}{x(x+1)}$+$\frac{1}{(x+1)(x+2)}$+…+$\frac{1}{(x+99)(x+100)}$;
(3)利用规律计算:$\frac{1}{x(x-1)}$+$\frac{1}{(x-1)(x-2)}$+…+$\frac{1}{(x-99)(x-100)}$.
分析 (1)观察已知等式,归纳总结得到一般性规律,写出第n个等式即可;
(2)原式利用得出的拆项方法变形,抵消合并即可得到结果;
(3)原式利用得出的拆项方法变形,抵消合并即可得到结果.
解答 解:(1)第n个式子为$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=$\frac{1}{x}$-$\frac{1}{x+1}$+$\frac{1}{x+1}$-$\frac{1}{x+2}$+…+$\frac{1}{x+99}$-$\frac{1}{x+100}$=$\frac{1}{x}$-$\frac{1}{x+100}$=$\frac{100}{x(x+100)}$;
(3)原式=$\frac{1}{x-1}$-$\frac{1}{x}$+$\frac{1}{x-2}$-$\frac{1}{x-1}$+$\frac{1}{x-100}$-$\frac{1}{x-99}$=$\frac{1}{x-100}$-$\frac{1}{x}$=$\frac{x-x+100}{x(x-100)}$=$\frac{100}{x(x-100)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
9.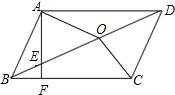 如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
 如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )
如图,在平行四边形ABCD中,∠ABD=50°,AF⊥BC于F,AF交BD于E,点O是DE的中点,连接OA,若DE=2AB,则∠ADB的大小是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
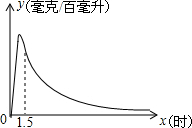 实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示).
实验数据显示:一般成人喝半斤低度白酒后,1.5小时内(包括1.5小时)其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=-200x2+400x表示;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=$\frac{k}{x}$(k>0)表示(如图所示). 已知,如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,O为交点,求证:点O到点A,B,C的距离相等.
已知,如图,直线l和直线m分别是线段AB和线段AC的垂直平分线,O为交点,求证:点O到点A,B,C的距离相等.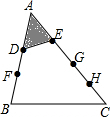 已知D、F和E、G、H把△ABC的两腰AB和AC分成三等分和四等分,已知阴影部分的小三角形的面积是15cm2,求△ABC的面积.
已知D、F和E、G、H把△ABC的两腰AB和AC分成三等分和四等分,已知阴影部分的小三角形的面积是15cm2,求△ABC的面积.