题目内容
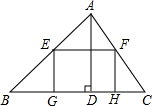 如图,有一块△ABC材料,BC=15,高AD=12,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,若EF=x,矩形EFGH的周长为y,
如图,有一块△ABC材料,BC=15,高AD=12,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,若EF=x,矩形EFGH的周长为y,(1)求y与x之间的函数关系式,并写出自变量的取值范围;
(2)求当矩形EFGH的周长为28时矩形的面积.
考点:相似三角形的应用
专题:
分析:(1)根据矩形的性质得出EF∥BC,得出相似三角形,推出比例式,求出MD的值,G根据0<EF<BC得出x的取值范围,进而得出结论;
(2)把矩形EFGH的周长为28求出x的值,根据三角形的面积公式得出结论.
(2)把矩形EFGH的周长为28求出x的值,根据三角形的面积公式得出结论.
解答: 解:(1)∵四边形EFGH是矩形,
解:(1)∵四边形EFGH是矩形,
∴EF∥BC,
∴△AEF∽△ABC,
∴
=
,即
=
,
解得MD=12-
x,
∴y=2(EF+MD)=2(x+12-
x)=24+
x,
∵矩形EFHG在△ABC内,
∴0<EF<BC,即0<x<15,
∴0<
x<6,
∴24<24+
x<30,即24<y<30;
(2)∵矩形EFGH的周长为28,
∴24+
x=28,解得x=10,
∴MD=12-
×10=4,
∴S矩形EFGH=10×4=40.
 解:(1)∵四边形EFGH是矩形,
解:(1)∵四边形EFGH是矩形,∴EF∥BC,
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AM |
| AD |
| x |
| 15 |
| 12-MD |
| 12 |
解得MD=12-
| 4 |
| 5 |
∴y=2(EF+MD)=2(x+12-
| 4 |
| 5 |
| 2 |
| 5 |
∵矩形EFHG在△ABC内,
∴0<EF<BC,即0<x<15,
∴0<
| 2 |
| 5 |
∴24<24+
| 2 |
| 5 |
(2)∵矩形EFGH的周长为28,
∴24+
| 2 |
| 5 |
∴MD=12-
| 4 |
| 5 |
∴S矩形EFGH=10×4=40.
点评:本题综合考查了相似三角形应用,不等式的性质,矩形的性质等知识点,此题有一点难度,对学生提出较高要求,但题型较好.

练习册系列答案
相关题目
 如图,已知点O为直线AB上一点,OE平分∠AOC,OF平分∠BOC,求∠EOF的度数.
如图,已知点O为直线AB上一点,OE平分∠AOC,OF平分∠BOC,求∠EOF的度数.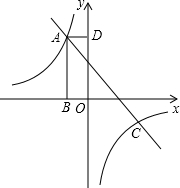 如图,矩形ABOD的顶点A是函数
如图,矩形ABOD的顶点A是函数