题目内容
10.关于x的一元二次方程kx2-2x+1=0有两个实数根x1,x2(1)求k的取值范围;
(2)若(kx12-x1+2)(kx22-x2+2)=2k,求k的值.
分析 (1)若一元二次方程有两个实数根,则根的判别式△=b2-4ac≥0,建立关于k的不等式,求出k的取值范围.还要注意二次项系数不为0;
(2)根据根与系数的关系得到x1+x2=$\frac{2}{k}$,x1x2=$\frac{1}{k}$,由于(kx12-x1+2)(kx22-x2+2)=2k可化为(x1+x2)+x1x2+1=2k,于是把x1+x2=$\frac{2}{k}$,x1x2=$\frac{1}{k}$代入(x1+x2)+x1x2+1=2k然后解方程即可.
解答 解:(1)∵关于x的一元二次方程kx2-2x+1=0有两个实数根,
∴根的判别式△=b2-4ac=4-4k≥0,且k≠0.
即k≤1且k≠0.
∴k的取值范围:k≤1且k≠0;
(2)根据题意得x1+x2=$\frac{2}{k}$,x1x2=$\frac{1}{k}$,
∵(kx12-x1+2)(kx22-x2+2)=2k可化为(x1+x2)+x1x2+1=2k,
∴$\frac{2}{k}$+$\frac{1}{k}$+1=2k,
解得:k=$\frac{3}{2}$,或k=-1,
∵k≤1且k≠0;
∴k=-1.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.也考查了一元二次方程的定义和根与系数的关系,切记不要忽略一元二次方程二次项系数不为零这一隐含条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标.
如图,已知△ABC,AB=AC,BC=6,BC边上的高AD垂直平分BC,且AD=4,以B为原点,BC所在直线为x轴,建立适当的平面直角坐标系,并求这个三角形三个顶点的坐标. 如图,D、E是以AB为直径的半圆O上任意两点,连接AD、AE、DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加的一个条件是①②③(填正确结论的序号).
如图,D、E是以AB为直径的半圆O上任意两点,连接AD、AE、DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加的一个条件是①②③(填正确结论的序号). 如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.
如图,在△ABC中,点O在AB上,以O为圆心的圆经过A,C两点,交AB于点D,已知∠A=α,∠B=β,且2α+β=90°.若OA=6,sinβ=$\frac{3}{5}$,求BC的长.
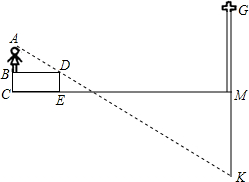 在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.
在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.