题目内容
14.Rt△ABC中,∠C=90°,AC=5,BC=12,则△ABC的内切圆半径为2.分析 设AB、BC、AC与⊙O的切点分别为D、F、E;易证得四边形OECF是正方形;那么根据切线长定理可得:CE=CF=$\frac{1}{2}$(AC+BC-AB),由此可求出r的长.
解答 解:如图: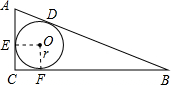
在Rt△ABC,∠C=90°,AC=5,BC=12,
根据勾股定理AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=13,
四边形OECF中,OE=OF,∠OEC=∠OFC=∠C=90°,
∴四边形OECF是正方形,
由切线长定理,得:AD=AE,BD=BF,CE=CF,
∴CE=CF=$\frac{1}{2}$(AC+BC-AB),
即:r=$\frac{1}{2}$(5+12-13)=2.
故答案为:2.
点评 此题主要考查了直角三角形内切圆的性质及半径的求法.根据已知得出CE=CF=$\frac{1}{2}$(AC+BC-AB)是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
2.有理数-$\frac{1}{3}$的相反数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
4.某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
(1)这个队队员年龄的众数是15,中位数是16;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
| 年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
| 人 数 | 1 | 4 | 3 | 2 | 2 |
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
 如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点.
如图是由7×7个边长为单位1的正方形组成的大正方形,每个小正方形顶点称为格点,请连结图中的格点. 一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.
一个印有“我喜欢数学课”字样的立方体纸盒表面展开图如图所示,则与印有“欢”字相对的表面上印有我字.