Question

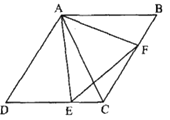
【题目】如图，O为菱形ABCD对角线的交点，M是射线CA上的一个动点（点M与点C、O、A都不重合），过点A、C分别向直线BM作垂线段，垂足分别为E、F，连接OE，OF．

（1）①依据题意补全图形；

②猜想OE与OF的数量关系为_________________.

（2）小东通过观察、实验发现点M在射线CA上运动时，（1）中的猜想始终成立．

小东把这个发现与同学们进行交流，通过讨论，形成了证明（1）中猜想的几种想法：

想法1：由已知条件和菱形对角线互相平分，可以构造与△OAE全等的三角形，从而得到相等的线段，再依据直角三角形斜边中线的性质，即可证明猜想；

想法2：由已知条件和菱形对角线互相垂直，能找到两组共斜边的直角三角形，例如其中的一组△OAB和△EAB，再依据直角三角形斜边中线的性质，菱形四边相等，可以构造一对以OE和OF为对应边的全等三角形，即可证明猜想．

……

请你参考上面的想法，帮助小东证明（1）中的猜想（一种方法即可）．

（3）当∠ADC=120°时，请直接写出线段CF，AE，EF之间的数量关系是_________________．

Answer 1

【答案】（1）①见解析；②OE=OF；（2）见解析；（3）EF=（CF+AE）

【解析】

（1）①由题意直接补全图形，②结论是OE=OF，
（2）方法1、先判断出△AOE≌△CON，再利用直角三角形的性质即可得出结论；
方法2、利用直角三角形斜边的中线等于斜边的一半，即可得出结论；
（3）先判断出四边形OPBQ是菱形，再判断出∠EOF=∠POQ=120°，再借助直角三角形的性质即可得出结论．

解：（1）①补全的图形如图所示．

②OE=OF．

（2）法一：

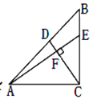
证明：如图1，

延长EO交FC的延长线于点N，

∵四边形ABCD是菱形，

∴AO=CO．

∵AE⊥BM，CF⊥BM，

∴AE∥CF．

∴∠AEO=∠CNO．

又∵∠AOE=∠CON，

∴△AOE≌△CON．

∴OE=ON=．

∵Rt△EFN中，O是斜边EN的中点，

∴OF=

∴OE=OF．

法二：

证明：如图2，

取线段AB，BC的中点P，Q，连接OP，PE，OQ，QF，

∵四边形ABCD是菱形，

∴AB=BC，AC⊥BD．

∵P，Q是AB，BC的中点，

∴OP=PB= ，OQ=QB=

∴OP=OQ．

同理，PE=QF．

∵OP=PB，PE=PB，

∴∠OPA=2∠OBA，∠EPA=2∠EBA．

∴∠OPA+∠EPA=2∠OBA+2∠EBA，即∠OPE=2∠OBE．

同理，∠OQF=2∠OCF．

∵AC⊥BD，CF⊥BM，

∴∠OBE+∠OMB=∠OCF+∠OMB=90°．

∴∠OBE=∠OCF．

∴∠OPE=∠OQF．

∴△OPE≌△OQF．

∴OE=OF．

（3）如图1，

由（2）方法一、得出△AOE≌△CON，

∴AE=CN，OE=ON，

由（2）知，OE=OF，∴OF=ON，

∵四边形ABCD是菱形，

∴∠ABC=∠ADC=120°，

∴∠ABE+∠CBF=60°，

∵∠AOB=∠AEB=90°，

∴点A、E、B、O共圆，

∴∠AOE=∠ABE，

同理：∠COF=∠CBF，

∴∠NOF=∠NOC+∠COF=∠AOE+∠CBF=∠ABE+∠CBF=60°，

∵OF=ON，

∴△FON是等边三角形，

∴∠ONF=60°，

∴∠FEN=30°，

在Rt△EFN中，∠FEN=30°，

∴EF=FN=（CF+CN）=（CF+AE）．

故答案为EF=（CF+AE）