Question

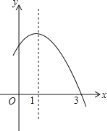
【题目】已知二次函数的部分图象如图所示，抛物线与轴的一个交点坐标为，对称轴为直线．

若，求的值；

若实数，比较与的大小，并说明理由．

Answer 1

【答案】；当时，，理由见解析.

【解析】

（1）已知抛物线对称轴为x=1，由抛物线对称性可知，其与x轴的另一个交点为（-1，0），把x=-1代入函数的解析式即可得到c-b的值；（2）当m≠1时，a+b＞m（am+b），把x=1和x=m分别代入函数的解析式得到关于a、b、c的关系式，因为顶点的横坐标为1，所以当x=1时函数取最大值y=a+b+c，即a+b+c＞am2+bm+c，进而证明a+b＞m（am+b）．

由抛物线对称性可知，其与轴的另一个交点为，

∴．

当时，解得．

当时，，

理由如下：

当时，，

当时，，

∵，

∴当时，函数取最大值，

∴当时，，

∴，

即．