题目内容
4.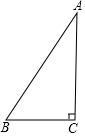 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.(1)尺规作图:作⊙O,使⊙O与AB、BC都相切,且圆心O在AC边上;(保留作图痕迹,不写作法)
(2)在(1)的条件下,设⊙O与AB的切点为D,⊙O的半径为3,且$\frac{AD}{BD}$=$\frac{2}{3}$,求AB的长.
分析 (1)利用角平分线的性质作出∠ABC的角平分线,利用角平分线上的点到角的两边距离相等得出,O点位置,进而得出答案.
(2)先设AD=2x,BD=3x,则BC=3x,AB=5x,根据勾股定理得出AC=4x,再根据勾股定理得到Rt△AOD中,(2x)2+32=(4x-3)2,解得x=2,进而得出AB的长.
解答 解:(1)作∠BAC的角平分线AP,交AC于点O,以O为圆心,OC为半径作圆,则⊙O即是所求图形.
(2)设AD=2x,BD=3x,则BC=3x,AB=5x,
∴Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4x,
∵DO=CO=3,
∴AO=4x-3,
∴Rt△AOD中,AD2+DO2=AO2,即(2x)2+32=(4x-3)2,
解得x=2,
∴AB=2×5=10.
点评 本题主要考查了复杂作图,切线的性质以及勾股定理的运用,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.已知四边形ABCD中,对角线AC与BD相交于点O,AD∥BC,下列判断中错误的是( )
| A. | 如果AB=CD,AC=BD,那么四边形ABCD是矩形 | |
| B. | 如果AB∥CD,AC=BD,那么四边形ABCD是矩形 | |
| C. | 如果AD=BC,AC⊥BD,那么四边形ABCD是菱形 | |
| D. | 如果OA=OC,AC⊥BD,那么四边形ABCD是菱形 |
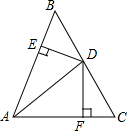 如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC.
如图,在△ABC中,AD平分∠CAB,D为BC的中点,DE⊥AB,DF⊥AC,垂足分别为E、F,求证:AD⊥BC. 如图,a、b为实数,化简|a+b|=-a-b.
如图,a、b为实数,化简|a+b|=-a-b.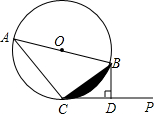 已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.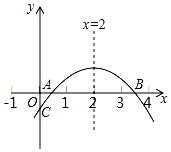 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论: