题目内容
如图，已知图中⊙O的半径为1，∠AOB=120°，则阴影部分的面积为
- A.
-
- B.
-
- C.-
- D.-
C
分析：分别求出△AOB及扇形AOB的面积，继而利用差值法可得出阴影部分的面积．
解答：过点O作OC⊥AB于点C，
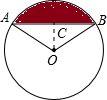
∵∠AOB=120°，OA=OB，
∴∠OAC=30°，
在Rt△OAC中，OC=
OA=，AC=
OC=，
则S△AOB=AB×OC=，S扇形AOB=
=，
故S阴影=S扇形AOB-S△AOB=-．
故选C．
点评：本题考查了扇形的面积计算，解答本题的关键是仔细观察图形，利用差值法求出不规则图形的面积．
分析：分别求出△AOB及扇形AOB的面积，继而利用差值法可得出阴影部分的面积．
解答：过点O作OC⊥AB于点C，
∵∠AOB=120°，OA=OB，
∴∠OAC=30°，
在Rt△OAC中，OC=
OA=，AC=OC=，则S△AOB=
AB×OC=，S扇形AOB==，故S阴影=S扇形AOB-S△AOB=
-．故选C．
点评：本题考查了扇形的面积计算，解答本题的关键是仔细观察图形，利用差值法求出不规则图形的面积．
练习册系列答案
相关题目
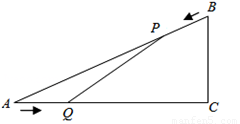
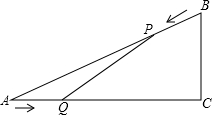（2013•天桥区一模）如图，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA向点A匀速运动，同时点Q由A出发沿AC向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．
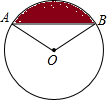（1997•广州）如图，已知图中⊙O的半径为1，∠AOB=120°，则阴影部分的面积为（ ）