��Ŀ����
��ͼ����֪��ABC�У�AB=10cm��AC=8cm��BC=6cm�������P��B������BA���A�����˶���ͬʱ��Q��A������AC���C�����˶������ǵ��ٶȾ�Ϊ2cm/s������PQ�����˶���ʱ��Ϊt����λ��s����0��t��4����
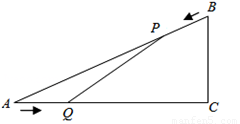
��1����tΪ��ֵʱ��PQ��BC��
��2�����AQP�����ΪS����λ��cm2������tΪ��ֵʱ��Sȡ�����ֵ����������ֵ��
��3���Ƿ����ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣������ڣ������ʱt��ֵ���������ڣ���˵�����ɣ�
��1�� s����2��t=
s����2��t= sʱ��Sȡ�����ֵΪ
sʱ��Sȡ�����ֵΪ cm2����3��������
cm2����3��������
��������
�����������1����PQ��BC�ɵ� ����
���� ��������ɣ�
��������ɣ�
��2���ȸ��ݹ��ɶ������涨��֤�á�C=90�㣬��P����PD��AC�ڵ�D����PD��BC�� ����
���� �����PD=6��
�����PD=6�� t�����ɵõ�S����t�Ķ��κ��������ݶ��κ��������ʼ�����ý����
t�����ɵõ�S����t�Ķ��κ��������ݶ��κ��������ʼ�����ý����
��3���������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�����S��AQP= S��ABC=12���ɣ�2����֪��S��AQP=��
S��ABC=12���ɣ�2����֪��S��AQP=�� t2+6t�����Щ�
t2+6t�����Щ� t2+6t=12�����ݴ˷����⣬���������жϣ�
t2+6t=12�����ݴ˷����⣬���������жϣ�
��1����PQ��BC
��
��
���t=
�൱t= sʱ��PQ��BC
sʱ��PQ��BC
��2����AB=10cm��AC=8cm��BC=6cm��
���C=90��
��P����PD��AC�ڵ�D��

��PD��BC��
�� ��
��
�� ��
��
���PD=6�� t
t
��S= ��AQ��PD=
��AQ��PD= ��2t����6��
��2t����6�� t��
t��
=�� t2+6t=��
t2+6t=�� ��t��
��t�� ��2+
��2+ ��
��
�൱t= sʱ��Sȡ�����ֵ�����ֵΪ
sʱ��Sȡ�����ֵ�����ֵΪ cm2
cm2
��3���������ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
����S��AQP= S��ABC=12��
S��ABC=12��
�ɣ�2����֪��S��AQP=�� t2+6t��
t2+6t��
�ੁ t2+6t=12��
t2+6t=12��
����ã�t2��5t+10=0��
�ߡ�=����5��2��4��1��10=��15��0���˷����⣬
�����ijʱ��t��ʹ�߶�PQǡ�ðѡ�ABC�����ƽ�֣�
���㣺������ۺ���
���������������ۺ���ǿ���ѶȽϴ����п��бȽϳ�����һ����Ϊѹ���⣬��Ŀ�Ƚϵ��ͣ�

 ��ͼ����֪��ABC�У�AB=AC��E��F�ֱ���AB��AC����AE=CF��
��ͼ����֪��ABC�У�AB=AC��E��F�ֱ���AB��AC����AE=CF�� ��ͼ����֪��ABC�У�P��AB��һ�㣬����CP���������������ж���ACP�ס�ABC���ǣ�������
��ͼ����֪��ABC�У�P��AB��һ�㣬����CP���������������ж���ACP�ס�ABC���ǣ������� ��2012•������һģ����ͼ����֪��ABC�У���C=90�㣬AC=4��BC=3����sinA=��������
��2012•������һģ����ͼ����֪��ABC�У���C=90�㣬AC=4��BC=3����sinA=�������� ��ͼ����֪��ABC�У�BC=8��BC���ϵĸ�h=4��DΪBC��һ�㣬EF��BC��AB��E����AC��F��EF����A��B������E��BC�ľ���Ϊx����DEF�����Ϊy����ôy����x�ĺ���ͼ������ǣ�������
��ͼ����֪��ABC�У�BC=8��BC���ϵĸ�h=4��DΪBC��һ�㣬EF��BC��AB��E����AC��F��EF����A��B������E��BC�ľ���Ϊx����DEF�����Ϊy����ôy����x�ĺ���ͼ������ǣ������� ��ͼ����֪��ABC�У�AB=AC��D��BC�е㣬�����н��۲���ȷ���ǣ�������
��ͼ����֪��ABC�У�AB=AC��D��BC�е㣬�����н��۲���ȷ���ǣ�������