题目内容
若九个正实数a,na,n2a,n3a,n4a,…,n8a满足a+na=
,n2a+n3a+n4a+n5a=15,则n6a+n7a+n8a= .
| 3 |
| 4 |
考点:因式分解的应用
专题:
分析:由a,na,n2a,n3a,n4a,…,n8a可以得出a>0,n>0,由a+na=
,n2a+n3a+n4a+n5a=15,得出n4+n2-20=0,解得n2=4或-5,由此得出n=2,进一步得出a=
,代入求得竖式即可.
| 3 |
| 4 |
| 1 |
| 4 |
解答:解:∵a,na,n2a,n3a,n4a,…,n8a是正实数,
∴a>0,n>0,
∵a+na=
,n2a+n3a+n4a+n5a=15
∴n2(a+na)+n4(a+na)=15
∴n4+n2-20=0,
解得n2=4或n2=-5(不合题意舍去),
∴n=2,n=-2(不合题意舍去),
∴a=
∴n6a+n7a+n8a=24+25+26=112.
故答案为:112.
∴a>0,n>0,
∵a+na=
| 3 |
| 4 |
∴n2(a+na)+n4(a+na)=15
∴n4+n2-20=0,
解得n2=4或n2=-5(不合题意舍去),
∴n=2,n=-2(不合题意舍去),
∴a=
| 1 |
| 4 |
∴n6a+n7a+n8a=24+25+26=112.
故答案为:112.
点评:此题考查因式分解的运用,一元二次方程的解法和代数式求值,合理分解,解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各数中:
,0,-
,
,0.3,0.3030030003…,
,无理数有( )
| 3 | -1 |
| 0.4 |
| 9 |
| 1 |
| π |
| A、0个 | B、1个 | C、2个 | D、3个 |
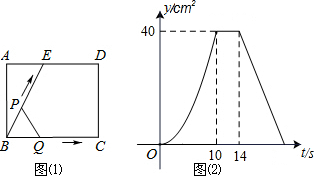 如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )| A、AE=8 | ||
B、当0≤t≤10时,y=
| ||
C、sin∠EBD=
| ||
| D、当t=12s时,△BPQ是等腰三角形 |
 已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积
已知:如图,有一块边长为8m正方形的土地,上面修了横纵各两条路,宽度都是1m,空白部分种上各种花草,则种花草的面积 如图,货轮与灯塔相距30海里,如何用方向和距离描述货轮相对于灯塔的位置
如图,货轮与灯塔相距30海里,如何用方向和距离描述货轮相对于灯塔的位置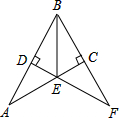 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=3,则BE的长是
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=3,则BE的长是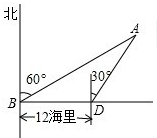 海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里后到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行.有没有触礁的危险?
海岛A的周围8海里内有暗礁,渔船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里后到达点D处,又测得海岛A位于北偏东30°,如果渔船不改变航向继续向东航行.有没有触礁的危险?