题目内容
19. 如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于B,AC⊥y轴于C,且△ABC的面积为2,则k=-4.
如图,点A在双曲线y=$\frac{k}{x}$上,AB⊥x轴于B,AC⊥y轴于C,且△ABC的面积为2,则k=-4.
分析 根据反比例函数系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,即可求解.
解答 解:∵AC⊥y轴于C点,AB⊥x轴于B点,∠BOC=90°,
∴四边形OBAC是矩形,
∴S△CBA=$\frac{1}{2}$S矩形OBAC.
∴S矩形OBAC=2S△ABC=4,
∴|k|=S矩形OBAC=4,
∵双曲线在第二象限,
∴k=-4,
故答案为:-4.
点评 本题主要考查了反比例函数系数k的几何意义,在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | (2ab)3=6a3b3 | C. | x2•x3=x6 | D. | (a3)2=a6 |
10.计算3-1的结果是( )
| A. | -1 | B. | -3 | C. | 3 | D. | $\frac{1}{3}$ |
14.直线y=2x+3与坐标轴围成的面积是( )
| A. | $\frac{3}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 6 |
 阅读材料:
阅读材料: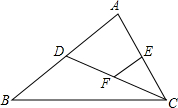 如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.
如图,CD是△ABC的中线,点E,F分别是AC、DC的中点,EF=2,则BD=4.