Question

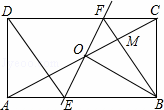
如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO．若∠COB=60°，FO=FC，则下列结论：

①FB⊥OC，OM=CM；

②△EOB≌△CMB；

③四边形EBFD是菱形；

④MB：OE=3：2．

其中正确结论的个数是（　　）

A．

1

B．

2

C．

3

D．

4

Answer 1

C

解：连接BD，

∵四边形ABCD是矩形，

∴AC=BD，AC、BD互相平分，

∵O为AC中点，

∴BD也过O点，

∴OB=OC，

∵∠COB=60°，OB=OC，

∴△OBC是等边三角形，

∴OB=BC=OC，∠OBC=60°，

在△OBF与△CBF中

∴△OBF≌△CBF（SSS），

∴△OBF与△CBF关于直线BF对称，

∴FB⊥OC，OM=CM；

∴①正确，

∵∠OBC=60°，

∴∠ABO=30°，

∵△OBF≌△CBF，

∴∠OBM=∠CBM=30°，

∴∠ABO=∠OBF，

∵AB∥CD，

∴∠OCF=∠OAE，

∵OA=OC，

易证△AOE≌△COF，

∴OE=OF，

∴OB⊥EF，

∴四边形EBFD是菱形，

∴③正确，

∴△EOB≌△FOB≌△FCB，

∴△EOB≌△CMB错误．

∵∠OMB=∠BOF=90°，∠OBF=30°，

∴MB=OM/，OF=OM/，

∵OE=OM，

∴MB：OE=3：2，正确；