题目内容
如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3 ,求⊙O 的半径长.
 |
(1)证明:连结OC(如图所示)
 则∠ACO=∠CAO (等腰三角形,两底角相等)
则∠ACO=∠CAO (等腰三角形,两底角相等)
∵CD切⊙O于C,∴CO⊥CD.
又∵AD⊥CD
∴AD∥CO
∴∠DAC=∠ACO (两直线平行,内错角相等)
∴∠DAC=∠CAO
∴AC平分∠BAD ----------------5分
(2)过点E画OE⊥AC于E(如图所示)
在Rt△ADC中,AD= =6
=6
∵OE⊥AC, ∴AE=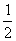 AC=
AC=
∵ ∠CAO =∠DAC,∠AEO =∠ADC =Rt∠
∴△AEO∽△ADC
∴ 即
即
∴AO= 即⊙O的半径为
即⊙O的半径为 . ----------------5分
. ----------------5分

练习册系列答案
相关题目
在函数y= 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
|
| A. | x≥0 | B. | x>0 | C. | x≠0 | D. | x>0且x≠1 |


 .如果在原有的棋子中再放进4颗黑色棋子,此时从盒子中随机取出
.如果在原有的棋子中再放进4颗黑色棋子,此时从盒子中随机取出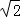 cm,则EF+CF的长为 ;
cm,则EF+CF的长为 ;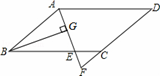
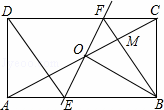
 ,则BE= 8 ,CD= 4或8 .
,则BE= 8 ,CD= 4或8 .