题目内容
已知抛物线y=a(x-h)2的形状与抛物线y=-2x2的形状相同,且顶点坐标为(-2,0),则a+h= .
考点:二次函数图象与几何变换
专题:
分析:已知抛物线y=a(x-h)2的形状与抛物线y=-2x2的形状相同,因而二次项系数的绝对值相同,因而二次项系数a是2或-2,顶点坐标为(-2,0),因而函数解析式是:y=±2(x+2)2,得到h=-2,进而求出a+h的值.
解答:解:已知抛物线的顶点坐标为(-2,0),可设此抛物线的解析式为y=a(x+2)2(a≠0),h=-2,由于抛物线和y=-2x2的图象形状相同,因此a=±2,所以a+h=0或-4.
故答案为0或-4.
故答案为0或-4.
点评:本题考查了二次函数图象与几何变换,熟记抛物线y=ax2+bx+c中,|a|的值确定抛物线的形状是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
当x>0,y>0时,下列正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列各方程,解是x=0的是( )
| A、7x-5=2x | ||||
| B、x-3=2x+1 | ||||
| C、4(5x-6)-7=9 | ||||
D、
|
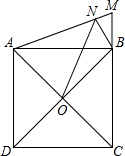 如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为
如图,正方形ABCD的边长为3,延长CB到点M,使BM=1,连接AM,过点B作BN⊥AM,垂足为N,O是对角线AC、BD的交点,连接ON,则ON的长为