题目内容
如图，以等腰直角△ABC两锐角顶点A、B为圆心作等圆，⊙A与⊙B恰好外切，若AC=2，那么图中两个扇形（即阴影部分）的面积之和为（ ）
|
| A． |
| B． |
| C． |
| D． |
|
考点：
扇形面积的计算；相切两圆的性质．
分析：
根据题意可判断⊙A与⊙B是等圆，再由直角三角形的两锐角互余，即可得到∠A+∠B=90°，根据扇形的面积公式即可求解．
解答：
解：∵⊙A与⊙B恰好外切，
∴⊙A与⊙B是等圆，
∵AC=2，△ABC是等腰直角三角形，
∴AB=2
，
∴两个扇形（即阴影部分）的面积之和=
+
=
=
πR2=
．
故选B．
点评：
本题考查了扇形的面积计算及相切两圆的性质，解答本题的关键是得出两扇形面积之和的表达式，难度一般．
练习册系列答案
相关题目
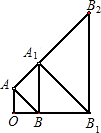如图，以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1，再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1，…，如此作下去，若OA=OB=1，则第2008个等腰直角三角形的面积S2008=
如图，以等腰直角三角形ABC的斜边AB与边面内作等边△ABD，连接DC，以DC当边作等边△DCE，B、E在C、D的同侧，若AB=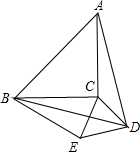
如图，以等腰直角三角形ABC的斜边AB为边向内作等边△ABD，连接DC，以DC为边作等边△DCE．B、E在C、D的同侧，若AB=
（2013•宁夏）如图，以等腰直角△ABC两锐角顶点A、B为圆心作等圆，⊙A与⊙B恰好外切，若AC=2，那么图中两个扇形（即阴影部分）的面积之和为（ ）
B．
C．
D．