题目内容
【题目】(理解新知)
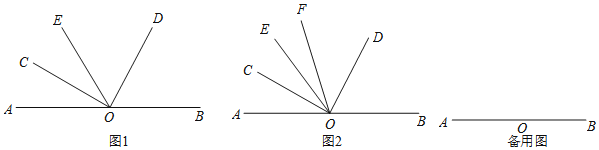
如图①,已知![]() ,在
,在![]() 内部画射线
内部画射线![]() ,得到三个角,分别为
,得到三个角,分别为![]() 、
、![]() 、
、![]() ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线![]() 为
为![]() 的“2倍角线”
的“2倍角线”
(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若![]() ,射线
,射线![]() 为
为![]() 的“2倍角线”,则
的“2倍角线”,则![]()
![]() ;
;
(解决问题)
如图②,已知![]() ,射线
,射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点逆时针旋转:射线
点逆时针旋转:射线![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 的速度绕
的速度绕![]() 点顺时针旋转,射线
点顺时针旋转,射线![]() 、
、![]() 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为![]() .
.
(3)当射线![]() 、
、![]() 旋转到同一条直线上时,求
旋转到同一条直线上时,求![]() 的值;
的值;
(4)若![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的![]() 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于![]() 的角.)
的角.)

【答案】(1)是(2)![]() 或
或![]() 或
或![]() (3)4,10,16,(4)2,12.
(3)4,10,16,(4)2,12.
【解析】
(1)根据2倍角线的定义即可求解;
(2)分3种情况,根据2倍角线的定义即可求解;
(3)分3种情况,根据2倍角线的定义得到方程求解即可;
(4)分情况,根据2倍角线的定义得到方程求解即可.
(1)角的平分线是这个角的“2倍角线”,
故答案为:是;
(2)∵射线![]() 为
为![]() 的“2倍角线”,
的“2倍角线”,
∴∠AOB=2∠AOC或∠AOC=2∠BOC或∠BOC=2∠AOC,
∵∠AOB=90°,∠AOC+∠BOC=∠AOB,
∴∠AOC=45°或∠AOC=60°或∠AOC=30°,
故答案为:45°或60°或30°;
(3)由题意得:运动时间范围为![]() ,
,
①![]() ,
,
![]() ,
,
②![]() ,
,
![]() ,
,
③![]() ,
,
![]() ,
,
综上,t的值为4或10或16;
(4)①![]() 为
为![]() 的“2倍角线”,此时
的“2倍角线”,此时![]() ,
,
![]() ,
,
![]() ,
,
②![]() 时,不存在,
时,不存在,
③![]() ,
,![]() 为
为![]() 的“2倍角线”,
的“2倍角线”,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
④![]() 不存在,
不存在,
综上:当![]() 、
、![]() 时,
时,![]() 、
、![]() 、
、![]() 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”.
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”.

练习册系列答案
相关题目