Question

【题目】如图，已知BC∥GE，AF∥DE，点D在直线BC上，点F在直线GE上，且∠1=50°．

（1）求∠AFG的度数；

（2）若AQ平分∠FAC，交直线BC于点Q，且∠Q=18°，则∠ACB的度数为______°．（直接写出答案）

Answer 1

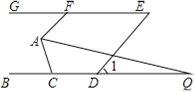
【答案】(1)50°；(2)86．

【解析】

（1）先根据BC∥EG得出∠E＝∠1＝50°，再由AF∥DE可知∠AFG＝∠E＝50°；

（2）作AM∥BC，由平行线的传递性可知AM∥EG，故∠FAM＝∠AFG，再根据AM∥BC可知∠QAM＝∠Q，故∠FAQ＝∠FAM＋∠QAM，再根据AQ平分∠FAC可知∠MAC＝∠QAC＋∠QAM＝86°，根据AM∥BC即可得出结论．

（1）∵BC∥EG，

∴∠E＝∠1＝50°．

∵AF∥DE，

∴∠AFG＝∠E＝50°；

（2）作AM∥BC，

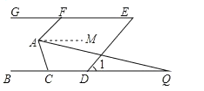
∵BC∥EG，

∴AM∥EG，

∴∠FAM＝∠AFG＝50°．

∵AM∥BC，

∴∠QAM＝∠Q＝18°，

∴∠FAQ＝∠FAM＋∠QAM＝68°．

∵AQ平分∠FAC，

∴∠QAC＝∠FAQ＝68°，

∴∠MAC＝∠QAC＋∠QAM＝86°．

∵AM∥BC，

∴∠ACB＝∠MAC＝86°

故答案为：86．