题目内容
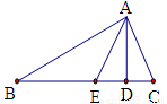
7. 如图所示,线段AB=6cm,C点从P点出发以1cm/s的速度沿AB向左运动,D点从B出发以2cm/s的速度沿AB向左运动(C在线段AP上,D在线段BP上)
如图所示,线段AB=6cm,C点从P点出发以1cm/s的速度沿AB向左运动,D点从B出发以2cm/s的速度沿AB向左运动(C在线段AP上,D在线段BP上)(1)若C,D运动到任意时刻都有PD=2AC,求出P在AB上的位置;
(2)在(1)的条件下,Q是直线AB上一点,若AQ-BQ=PQ,求PQ的值;
(3)在(1)的条件下,若C,D运动了一段时间后恰有AB=2CD,这时点C停止运动,点继续在线段PB上运动,M,N分别是CD,PD的中点,求出MN的值.
分析 (1)根据C、D的运动速度知BD=2PC,再由已知条件PD=2AC求得PB=2AP,所以点P在线段AB上的$\frac{1}{3}$处;
(2)由题设画出图示,根据AQ-BQ=PQ求得AQ=PQ+BQ;然后求得AP=BQ,从而求得PQ与AB的关系;
(3)当C点停止运动时,有CD=$\frac{1}{2}$AB,故AC+BD=$\frac{1}{2}$AB,所以AP-PC+BD=$\frac{1}{2}$AB,再由AP=$\frac{1}{3}$AB,PC=5cm,BD=10cm,再根据M是CD中点,N是PD中点可得出MN的长,进而可得出结论.
解答 解:(1)根据C、D的运动速度知:BD=2PC.
∵PD=2AC,
∴BD+PD=2(PC+AC),即PB=2AP,
∴点P在线段AB上的$\frac{1}{3}$处;
(2)如图1:
∵AQ-BQ=PQ,
∴AQ=PQ+BQ;
又∵AQ=AP+PQ,
∴AP=BQ,
∴PQ=$\frac{1}{3}$AB=2cm;
当点Q'在AB的延长线上时,
AQ′-AP=PQ′,
所以AQ′-BQ′=PQ=AB=6cm.
综上所述,PQ=2cm或6cm.
(3)MN的值不变. 理由:如图2,当C点停止运动时,有CD=$\frac{1}{2}$AB=3cm,
理由:如图2,当C点停止运动时,有CD=$\frac{1}{2}$AB=3cm,
∴AC+BD=$\frac{1}{2}$AB=3cm,
∴AP-PC+BD=$\frac{1}{2}$AB=3cm,
∵AP=$\frac{1}{3}$AB=2cm,PC=5cm,
∵M是CD中点,N是PD中点,
∴MN=MD-ND=$\frac{1}{2}$CD-$\frac{1}{2}$PD=$\frac{1}{2}$CP=$\frac{1}{2}$cm.
点评 本题考查了一元一次方程的应用,两点间的距离,灵活运用线段的和、差、倍、分转化线段之间的数量关系是十分关键的一点.

| A. | -$\frac{{b}^{3}}{2{a}^{3}}$ | B. | -$\frac{{b}^{3}}{6{a}^{3}}$ | C. | -$\frac{{b}^{3}}{8{a}^{3}}$ | D. | $\frac{{b}^{3}}{8{a}^{3}}$ |
 如图是使用五个相同的立方体搭成的几何体,其左视图是( )
如图是使用五个相同的立方体搭成的几何体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | y1>0,y2<0 | B. | y1<0,y2<0 | C. | y1•y2<0 | D. | y1+y2<0 |
 如图,在平行四边形ABCD中,P、Q是对角线BD上的两个点,且BP=DQ.
如图,在平行四边形ABCD中,P、Q是对角线BD上的两个点,且BP=DQ. △ABC中,EF∥BC,E在AB上,F在AC上,若$\frac{AE}{EB}$=$\frac{2}{3}$,则EF:BC=2:5.
△ABC中,EF∥BC,E在AB上,F在AC上,若$\frac{AE}{EB}$=$\frac{2}{3}$,则EF:BC=2:5.