题目内容
(本题满分10分)如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).

(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请求出点Q 坐标;如果不存在,请说明理由.
(1)作图见试题解析;(2)P(1,﹣1);(3)存在,Q(﹣2,﹣2),(2,﹣4).
【解析】
试题分析:(1)作出AC与BC线段垂直平分线得出交点即为圆心,进而利用圆心到线段端点距离长为半径求出即可;
(2)过点P做PD⊥x轴,PE⊥y轴,垂足分别为D、E,连接PC、PE,在Rt△BPD中,BP2=x2+32,在Rt△CEP中,CP2=(x+2)2+12,由BP=CP,求出x的值,即可得出P点坐标;
(3)利用相似三角形的判定得出△Q1BC∽△ACO,进而结合圆周角定理得出Q点坐标.
试题解析:(1)如图1所示:

(2)如图2,过点P做PD⊥x轴,PE⊥y轴,垂足分别为D、E,连接PC、PE.
∵PD⊥AB,∴AD=BD=3,
∵OB=4,∴OD=OB﹣BD=1,∴PE=OD=1,
设DP=x,则OE=PD=x,在Rt△BPD中, .
.
在Rt△CEP中, ,
,
∵BP=CP,∴ ,解得:
,解得: .∴点P坐标为(1,﹣1);
.∴点P坐标为(1,﹣1);
(3)如图2,连接BP并延长到⊙P于一点Q1,连接CQ1,则BQ1是直径,∴∠Q1CB=90°,
又∵∠CAB=∠CQ1B,∴△Q1BC∽△ACO,
此时连接AQ1,则∠Q1AB=90°,∴Q1横坐标为:﹣2,
∵AB=6,BQ1=2BP= ,∴AQ1=2,∴Q1(﹣2,﹣2),
,∴AQ1=2,∴Q1(﹣2,﹣2),
同理构造直角三角形CFQ2,可得出:CF=6,CQ2= ,∴FQ2=2,FO=4,则Q2(2,﹣4),
,∴FQ2=2,FO=4,则Q2(2,﹣4),
综上所述:)⊙P上存在一点Q(﹣2,﹣2),(2,﹣4),使得△QBC与△AOC相似.

考点:圆的综合题.

 53天天练系列答案
53天天练系列答案

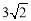 ,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则线段PQ的最小值为( )
 B.2 C.
B.2 C. D.
D. 时,原方程应变形为( )
时,原方程应变形为( ) B.
B. C.
C. D.
D.

 (精确到0.01).
(精确到0.01).
 的距离为3,点P是直线
的距离为3,点P是直线 上的一个动点,PQ切⊙O于点Q,则PQ的最小值是( )
上的一个动点,PQ切⊙O于点Q,则PQ的最小值是( )
 B.
B. C.3 D.2
C.3 D.2