题目内容
9.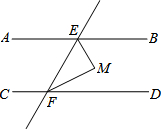 如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )
如图,直线AB∥CD,EF分别交AB、CD于点E、F,EM平分∠BEF,FM平分∠DFE,则∠EMF的度数为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
分析 由于AB∥CD,那么直线AB、CD被直线EF所截得的同旁内角∠BEF、∠DFE互补,而ME、MF分别平分两角,故∠MEF、∠MFE的度数和为∠BEF、∠DFE的度数和的一半,于是得到结论.
解答 解:∵AB∥CD,
∴∠BEF+∠DFE=180°;
∵ME平分∠BEF、MF平分∠DFE,
∴∠BEM=∠MEF,∠DFM=∠MFE,
∴∠MEF+∠MFE=$\frac{1}{2}$(∠BEF+∠DFE)=90°,
∴∠EMF=90°.
故选C.
点评 本题考查综合运用平行线的性质、角平分线的定义、三角形内角和等知识解决问题的能力.

练习册系列答案
相关题目
19.某市的出租车的起步价为10元(行驶不超过3千米),以后每增加1千米,加价1.8元,现在某人乘出租车行驶P千米的路程(P>3)所需费用是( )
| A. | 10+1.8P | B. | 1.8P | C. | 10-1.8P | D. | 10+1.8(P-3) |
20.如果a与6互为相反数,那么-(-a)的值为( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | -$\frac{1}{6}$ |
17.若等式$\sqrt{2}$□$\sqrt{2}$=2成立,则□内的运算符号是( )
| A. | + | B. | - | C. | × | D. | ÷ |
14.从n边形一个顶点出发,可以作( )条对角线.
| A. | n | B. | n-1 | C. | n-2 | D. | n-3 |
 如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N.若∠AOB=30°,则∠P1OP2=60°.
如图,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2,连接P1P2交OA于M,交OB于N.若∠AOB=30°,则∠P1OP2=60°.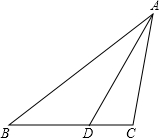 如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD.
如图,在△ABC中,AC=BC,∠ACB=100°,AD是角平分线.求证:AB=AD+CD. 如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9.
如图,在⊙O中,∠ACB=∠D=60°,AC=3,则⊙O的直径为9.