题目内容
15.汽车在上坡时速度为28千米/时,下坡时速度为42千米/时,从甲地到乙地用了4$\frac{1}{2}$小时,返回时用了4$\frac{2}{3}$小时,从甲地到乙地上、下坡各是多少千米?分析 首先设从甲地到乙地上坡xkm,下坡是y千米,利用从甲地到乙地用了4$\frac{1}{2}$小时,返回时用了4$\frac{2}{3}$小时,分别得出等式求出答案即可.
解答 解:设从甲地到乙地上坡xkm,下坡是y千米,根据题意可得:
$\left\{\begin{array}{l}{\frac{x}{28}+\frac{y}{42}=4\frac{1}{2}}\\{\frac{x}{42}+\frac{y}{28}=4\frac{2}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=70}\\{y=84}\end{array}\right.$,
答:从甲地到乙地上坡70km,下坡是84千米.
点评 此题主要考查了二元一次方程组的应用,根据题意得出正确等量关系是解题关键.

练习册系列答案
相关题目
6.已知a=$\sqrt{2}$,b=$\sqrt{5}$,则$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}÷\frac{1}{a}$的值为( )
| A. | $\sqrt{5}-\sqrt{2}$ | B. | 3 | C. | $\sqrt{2}+\sqrt{5}$ | D. | $\sqrt{2}-\sqrt{5}$ |
9.如图是一个简单的数值运算程序,当输出y的值为-1时,则输入x的值为( )


| A. | 1 | B. | 5 | C. | -1 | D. | ±1 |
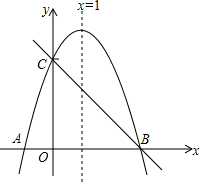 如图,抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线
如图,抛物线y=ax2+bx+c交x轴于A,B两点,交y轴于点C,已知抛物线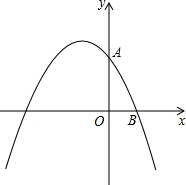 如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.
如图,已知点A(0,4)和点B(3,0)都在抛物线y=mx2+2mx+n上.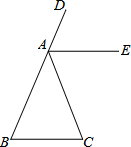 如图,已知∠DAC是△ABC的一个外角,请在下列三个关系:
如图,已知∠DAC是△ABC的一个外角,请在下列三个关系: