题目内容
16．
如图，是二次函数y=ax2+bx+c的图象，则下列判断正确的有（ ）①abc＜0
②4a+2b+c＞0
③9a+3b+c＞0
④3a+c＜0．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 根据二次函数的图象求出a＜0，c＞0，根据抛物线的对称轴求出b=-2a＞0，即可得出abc＜0，可判断①；令x=2，结合图象可判断②；把x=3代入二次函数得出y=9a+3b+c=0，可判断③；把x=-1代入得出y=a-b+c=3a+c＜0，根据图象可判断④．
解答 解：∵二次函数的图象开口向下，图象与y轴交于y轴的正半轴上，
∴a＜0，c＞0，
∵抛物线的对称轴是直线x=1，
∴-$\frac{b}{2a}$=1，
∴b=-2a＞0，
∴abc＜0，故①选项正确；
把x=2代入二次函数得出y=4a+2b+c＞0，
故②选项正确；
把x=3代入二次函数y=ax2+bx+c（a≠0）得：y=9a+3b+c＜0，故③选项错误；
∵b=-2a
∴把x=-1代入得出y=a-b+c=3a+c＜0，故④选项正确．
所以正确的选项为①②④共3个，
故选C．
点评 本题考查了二次函数的图象、性质，二次函数图象与系数的关系，结合图象确定函数值是解答此题的关键．
练习册系列答案
相关题目
6．下列关于平方根说法和等式中正确的是（ ）
| A． | $\sqrt{\frac{4}{25}}=±\frac{2}{5}$ | B． | $\sqrt{{{（{-3}）}^2}}=-3$ | C． | -a2没有平方根 | D． | $-\sqrt{{{（{-4}）}^2}}=-4$ |
7．
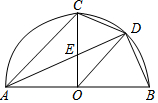如图AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下5个结论：
①OD∥AC；
②AC=2CD；
③2CD2=CE•AB；
④S△AEC=2S△DEO；
⑤线段OD是DE与DA的比例中项．
其中正确结论的序号（ ）
如图AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB分别交OC于点E，交弧BC于点D，连结CD、OD，给出以下5个结论：①OD∥AC；
②AC=2CD；
③2CD2=CE•AB；
④S△AEC=2S△DEO；
⑤线段OD是DE与DA的比例中项．
其中正确结论的序号（ ）
| A． | ①②③ | B． | ①④⑤ | C． | ①③④ | D． | ①③④⑤ |
11．a是一个两位数，b是一个三位数，把a放在b的右边组成一个五位数，用a，b的代数式表示所得的五位数是（ ）
| A． | ba | B． | 10b+a | C． | 10000b+a | D． | 100b+a |
1．下列图形中，是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
8．已知代数式2x2-3x-9的值为9，则x2-$\frac{3}{2}$x-9的值为（ ）
| A． | $-\frac{9}{2}$ | B． | $\frac{9}{2}$ | C． | 0 | D． | -9 |
5．近似数2.70所表示的准确数a的取值范是（ ）
| A． | 2.695≤a＜2.705 | B． | 2.65≤a＜2.75 | C． | 2.695＜a≤2.705 | D． | 2.65＜a≤2.75 |
将一直角三角板与两边平行的硬纸条如图所示放置，下列结论：