Question

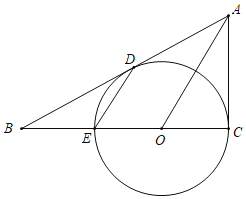
【题目】如图，已知点、在直线上，且，于点，且，以为直径在的左侧作半圆，于，且.

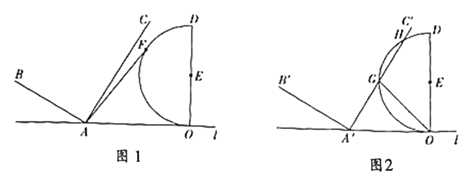
（1）若半圆上有一点，则的最大值为________；

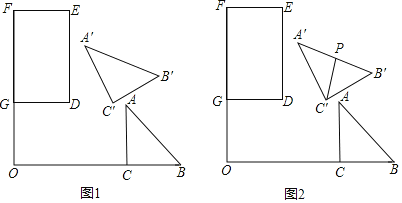
（2）向右沿直线平移得到；

①如图，若截半圆的的长为，求的度数；

②当半圆与的边相切时，求平移距离.

Answer 1

【答案】（1）；（2）①；②

【解析】

（1）由图可知当点F与点D重合时，AF最大，根据勾股定理即可求出此时AF的长；

（2）①连接EG、EH．根据的长为π可求得∠GEH=60°，可得△GEH是等边三角形，根据等边三角形的三个角都等于60°得出∠HGE=60°，可得EG//A'O，求得∠GEO=90°，得出△GEO是等腰直角三角形，求得∠EGO=45°，根据平角的定义即可求出∠A'GO的度数；

②分C'A'与半圆相切和B'A'与半圆相切两种情况进行讨论，利用切线的性质、勾股定理、切斜长定理等知识进行解答即可得出答案．

解：

（1）当点F与点D重合时，AF最大，

AF最大=AD==，

故答案为：；

（2）①连接、.

∵，

∴.

∵，

∴是等边三角形，

∴.

∵，

∴，

∴，

∵，

∴，

∵，

∴，

∴.

②当切半圆于时，连接，则.

∵，

∴切半圆于点，

∴.

∵，

∴，

∴平移距离为.

当切半圆于时，连接并延长于点，

∵，，，

∴，

∵，

∴，

∵，

∴，

∵，

∴.

∵，

∴.