题目内容
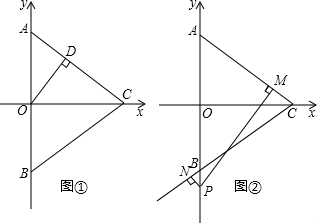
如图1,点A,B的坐标分别为A(0,3),B(0,-3),点C(m,0)为x轴正半轴上一点.
(1)求证:AC=BC;
(2)如图①,若m满足(m+5)(m+6)-(m+4)(m+5)=18,过O作OD⊥AC于D点,求OD•AC的值;
(3)如图②,在(2)的条件下,点P为线段OB的延长线上的一动点,当点P为线段OB的延长线上向下运动时,作PM⊥AC于M点,PN⊥BC于N点,式子AC(PM-PN)的值是否发生改变?若不变,求出其值;若变化,求出其值的变化范围.
(1)求证:AC=BC;
(2)如图①,若m满足(m+5)(m+6)-(m+4)(m+5)=18,过O作OD⊥AC于D点,求OD•AC的值;
(3)如图②,在(2)的条件下,点P为线段OB的延长线上的一动点,当点P为线段OB的延长线上向下运动时,作PM⊥AC于M点,PN⊥BC于N点,式子AC(PM-PN)的值是否发生改变?若不变,求出其值;若变化,求出其值的变化范围.

考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:(1)根据勾股定理可以求得AC2=BC2,即可解题;
(2)根据题干中给出等式可以求得m的值,根据三角形面积公式即可求得AC•OD=OA•OC,即可解题;
(3)根据m=4,可以求得AC,BC的解析式,即可求得PM,PN的值,对a分类讨论即可解题.
(2)根据题干中给出等式可以求得m的值,根据三角形面积公式即可求得AC•OD=OA•OC,即可解题;
(3)根据m=4,可以求得AC,BC的解析式,即可求得PM,PN的值,对a分类讨论即可解题.
解答:(1)证明:∵AC2=OC2+AO2,BC2=BO2+OC2,AO=BO=3,
∴AC2=BC2,
∴AC=BC;
(2)解:∵(m+5)(m+6)-(m+4)(m+5)=18,
整理得:2m+10=18,
∴m=4,
∵
AC•OD=
OA•OC,
∴AC•OD=OA•OC=12;
(3)解:由(2)知,m=4,
则AC=5,
设AC的方程为y=kx+b,将A,C两点代入得直线AC方程为:3x+4y-12=0,
设BC方程为y=px+q,将B,C代入得BC的方程为-3x+4y+12=0,
设P点(0,a),(a<0)
则PM=
,
PN=
,
故AC(PM-PN)=12-4a-|4a+12|,
当a<-3时,原式=-8a,
当-3<a<0时,原式=24.
∴AC2=BC2,
∴AC=BC;
(2)解:∵(m+5)(m+6)-(m+4)(m+5)=18,
整理得:2m+10=18,
∴m=4,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AC•OD=OA•OC=12;
(3)解:由(2)知,m=4,
则AC=5,
设AC的方程为y=kx+b,将A,C两点代入得直线AC方程为:3x+4y-12=0,
设BC方程为y=px+q,将B,C代入得BC的方程为-3x+4y+12=0,
设P点(0,a),(a<0)
则PM=
| |4a-12| |
| 5 |
PN=
| |4a+12| |
| 5 |
故AC(PM-PN)=12-4a-|4a+12|,
当a<-3时,原式=-8a,
当-3<a<0时,原式=24.
点评:本题考查了勾股定理的运用,考查了三角形面积的计算,考查了点到直线距离的求解,本题中求得直线AC,BC解析式是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
下列说法不正确的是( )
| A、a2•a4=a6 |
| B、a3•a3=a6 |
| C、(-x)2•(-x)3=(-x)5 |
| D、z2•z3=z6 |
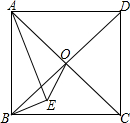 如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2
如图,在正方形ABCD内有一点E,∠AEB=90°,AE=2 如图是由四个相同的小立方块搭成的几何体.每一个小立方体的六个面分别涂着红、黄、蓝、白、黑、紫色,从这个图可知,最上面一个小立方块的左面涂
如图是由四个相同的小立方块搭成的几何体.每一个小立方体的六个面分别涂着红、黄、蓝、白、黑、紫色,从这个图可知,最上面一个小立方块的左面涂