题目内容
等腰三角形一腰上的中线把这个三角形的周长分成为12cm和15cm两部分,则此三角形的底边长为 .
考点:等腰三角形的性质
专题:分类讨论
分析:根据题意画出图形,分情况讨论当AB+AD为15cm,BC+CD为12cm时,AB+AD为12cm,BC+CD为15cm时,设腰长为xcm,底边长为ycm,根据等腰三角形的性质列出方程组,求出值后检验是否可以组成三角形.
解答: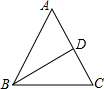 解:①当AB+AD为15cm,BC+CD为12cm时,
解:①当AB+AD为15cm,BC+CD为12cm时,
设腰AB长为xcm,底边CB长为ycm,则:
,
解得:
,
经检验符合题意;
②AB+AD为12cm,BC+CD为15cm时,
设腰AB长为xcm,底边CB长为ycm,则:
,
解得:
,
经检验符合题意.
故答案为:11cm或7cm.
 解:①当AB+AD为15cm,BC+CD为12cm时,
解:①当AB+AD为15cm,BC+CD为12cm时,设腰AB长为xcm,底边CB长为ycm,则:
|
解得:
|
经检验符合题意;
②AB+AD为12cm,BC+CD为15cm时,
设腰AB长为xcm,底边CB长为ycm,则:
|
解得:
|
经检验符合题意.
故答案为:11cm或7cm.
点评:此题主要考查了等腰三角形的性质和三角形的三边关系;题目从边的方面考查三角形,涉及分类讨论的思想方法.列出方程组是正确解答本题的关键.

练习册系列答案
相关题目
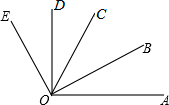 如图,OB是∠AOC的角平分线,OD是∠COE的角平分线.
如图,OB是∠AOC的角平分线,OD是∠COE的角平分线. 如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为
如图,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠CFE为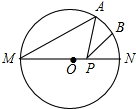 如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为
如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为