题目内容
8.若二次函数y=-x2+2(k-1)x+2k-k2的图象经过原点,求:(1)二次函数的解析式;
(2)它的图象与x轴交点O、Q及顶点C组成的△OAC的面积.
分析 (1)直接把原点坐标代入二次函数解析式中得到关于k的方程,然后解方程即可求得k,即可求得解析式;
(2)画出函数图形,得出交点O、A及顶点C,利用三角形的面积求得答案即可.
解答 解:(1)把(0,0)代入y=-x2+2(k-1)x+2k-k2得
2k-k2=0
解得:k=0或k=2,
所以二次函数的解析式为y=-x2-2x或y=-x2+2x.
(2)如图,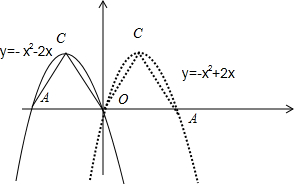
当y=-x2-2x时,
△OAC的面积=$\frac{1}{2}$×2×1=1;
或y=-x2+2x,
△OAC的面积=$\frac{1}{2}$×2×1=1.
点评 此题考查了运用待定系数法求二次函数解析式,在坐标系中求三角形面积的问题;解题的方法是将所给的函数图象上点的坐标直接代入函数解析式,求得关键点,利用面积计算公式求得答案.

练习册系列答案
相关题目
3. 如图,数轴上表示数-2的相反数的点是( )
如图,数轴上表示数-2的相反数的点是( )
 如图,数轴上表示数-2的相反数的点是( )
如图,数轴上表示数-2的相反数的点是( )| A. | 点N | B. | 点M | C. | 点Q | D. | 点P |
 如图,A、O、B三点在同一直线上,OD是∠AOC的平分线,OE是∠BOC的平分线
如图,A、O、B三点在同一直线上,OD是∠AOC的平分线,OE是∠BOC的平分线