Question

8．如图所示，矩形ABCD中，AB=6，AD=3，点O在边DC上，且DO=4，点P，Q同时从点O出发，点P沿OA以1cm/s的速度移动，点Q沿O→C→B→A的路线以2cm/s的速度移动，当点P移动到点A时，点Q也停止移动．
（1）求sin∠AOD的值；
（2）设点P移动时间为t（s），P，Q两点运动路线与线段PQ围成的图形面积为S．
①当t=1s时，点Q到达C点．
②求S与t的函数关系式．

Answer 1

分析 （1）由矩形的性质得出∠D=∠C=∠B=90°，CD=AB=6，BC=AD=3，得出DO=3，由勾股定理求出OA=5，由三角函数定义即可得出结果；
（2）①求出OC=CD-DO=2，即可得出t的值；
②分三种情况：当0≤t≤1时，作PM⊥CD于M，则PM=$\frac{3}{5}$t，OQ=2t，S=△OPQ的面积，即可得出答案；
当1＜t≤2.5时，作PM⊥CD于M，则PM=$\frac{3}{5}$t，OM=$\frac{4}{5}$t，CQ=2t-2，S=梯形CQPM的面积-△OPM的面积，即可得出答案；
当2.5＜t≤5时，作PN⊥AB于N，则BQ=2t-5，PN=3-$\frac{3}{5}$t，AQ=AB-BQ=11-2t，S=梯形ABCO的面积-△APQ的面积，即可得出答案．

解答 解：（1）∵四边形ABCD是矩形，
∴∠D=∠C=∠B=90°，CD=AB=6，BC=AD=3，
∵DO=3，
∴OA=$\sqrt{A{D}^{2}+D{O}^{2}}$=5，
∴sin∠AOD=$\frac{AD}{OA}$=$\frac{3}{5}$；
（2）①∵OC=CD-DO=2，点Q沿O→C→B→A的路线以2cm/s的速度移动，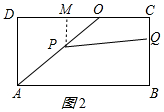
∴t=2÷2=1（s），
即t=1s时，点Q到达C点；
故答案为：1；
②当0≤t≤1时，如图1所示：
作PM⊥CD于M，则PM=$\frac{3}{5}$t，OQ=2t，
∴S=△OPQ的面积=$\frac{1}{2}$•2t•$\frac{3}{5}$t=$\frac{3}{5}$t²；
当1＜t≤2.5时，如图2所示：
作PM⊥CD于M，则PM=$\frac{3}{5}$t，OM=$\frac{4}{5}$t，CQ=2t-2，
S=梯形CQPM的面积-△OPM的面积=$\frac{1}{2}$（2t-2+$\frac{3}{5}$t）（$\frac{4}{5}$t+2）-$\frac{1}{2}$•$\frac{4}{5}$t•$\frac{3}{5}$t=$\frac{4}{5}$t²+$\frac{9}{5}$t-2；
当2.5＜t≤5时，如图3所示：
作PN⊥AB于N，则BQ=2t-5，PN=3-$\frac{3}{5}$t，AQ=AB-BQ=11-2t，
∴S=梯形ABCO的面积-△APQ的面积=$\frac{1}{2}$（2+6）×3-$\frac{1}{2}$（11-2t）（3-$\frac{3}{5}$t）=-$\frac{3}{5}$t²+$\frac{63}{10}$t-$\frac{9}{2}$．

点评 本题是四边形综合题目，考查了矩形的性质、勾股定理、三角函数、动点问题、三角形面积以及梯形面积的计算；本题综合性强，有一定难度，进行分类讨论是解决问题（2）的关键．