题目内容
 如图,在△ABC中,AD是BC边上的高,E、F分别是AB、AC的中点,△DEF与△ABC相似吗?
如图,在△ABC中,AD是BC边上的高,E、F分别是AB、AC的中点,△DEF与△ABC相似吗?考点:相似三角形的判定
专题:
分析:首先利用相似三角形的判定方法得出△AEF∽△ABC,进而利用线段垂直平分线的性质得出EA=ED,FA=FD,求出△AEF≌△DEF(SSS),进而得出答案.
解答:解:△DEF与△ABC相似,
理由:∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴△AEF∽△ABC,
∵AD是BC边上的高,EF是△ABC的中位线,
∴EF平分AD,EF⊥AD,
∴EA=ED,FA=FD,
在△AEF和△DEF中
,
∴△AEF≌△DEF(SSS),
∴△DEF∽△ABC.
理由:∵E、F分别是AB、AC的中点,
∴EF∥BC,
∴△AEF∽△ABC,
∵AD是BC边上的高,EF是△ABC的中位线,
∴EF平分AD,EF⊥AD,
∴EA=ED,FA=FD,
在△AEF和△DEF中
|
∴△AEF≌△DEF(SSS),
∴△DEF∽△ABC.
点评:此题主要考查了相似三角形的判定与性质以及全等三角形的判定,得出△AEF≌△DEF是解题关键.

练习册系列答案
相关题目
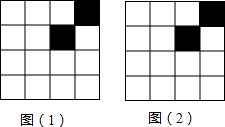 如图,在“4×4”正方形网格中,已有2个小正形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).
如图,在“4×4”正方形网格中,已有2个小正形被涂黑.请你分别在下面2张图中再将若干个空白的小正方形涂黑,使得涂黑的图形成为轴对称图形.(图(1)要求只有1条对称轴,图(2)要求只有2条对称轴).
 画出如图所示的几何体的主视图和左视图.
画出如图所示的几何体的主视图和左视图.