题目内容
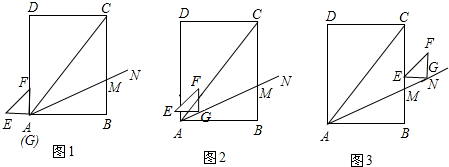
7.在平面直角坐标系中,正方形OABC的两边OA、OC分别落在x轴、y轴的正半轴上,等腰Rt△ADE的两个顶点D、E和正方形顶点B三点在一条直线上.(1)如图1,连接OD,求证:△OAD≌△BAE;
(2)如图2,连接CD,求证:BE-$\frac{1}{2}$DE=$\frac{\sqrt{2}}{2}$CD;
(3)如图3,当图1中的Rt△ADE的顶点D与点B重合时,点E正好落在x轴上,F为线段OC上一动点(不与O、C重合),G为线段AF的中点,若CG⊥GK交BE于点K时,请问∠KCG的大小是否变化?若不变,请求其值;若改变,求出变化的范围.

分析 (1)利用同角的余角相等可得∠BAD=∠EAF,由此得∠OAD=∠BAE,根据SAS证明△OAD≌△BAE;
(2)作辅助线构建正方形ANDM和等腰直角三角形CFD,把所求CD转化为CF,证CF=OM,由(1)中的全等可知∠ODA=∠BEA=45°,证明∠ODC=45°,推出CF与CD的关系,利用直角三角形斜边中线和正方形的性质求出BE-$\frac{1}{2}$DE的值为OM,得出结论;
(3)作辅助线构建正方形BMKN和全等三角形,首先利用全等证明CG=QG,由线段垂直平分线性质得KC=KQ,证明Rt△CNK≌Rt△QMK,得∠CKN=∠QKM,可知∠CKQ=90°,得△KCQ是等腰直角三角形,因此得出结论:∠KCG的大小不变,等于45°.
解答 证明:(1)如图1,在正方形ABCO中,
∵∠BAF=∠DAE=90°,
∴∠BAD=∠EAF,
∴∠BAD+∠OAB=∠EAF+∠BAF,
即∠OAD=∠BAE,
∵AB=AO,AD=AE,
∴△OAD≌△BAE;
(2)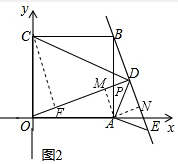 如图2,设CD与AB的交点为P,
如图2,设CD与AB的交点为P,
过C作CF⊥OD于F,过A作AN⊥DE于N,AM⊥OD于M,
∵等腰Rt△ADE,AD=AE,
∴AN=DN=$\frac{1}{2}$DE,
∴四边形ANDM是正方形,
∴DN=DM,
∴BE-$\frac{1}{2}$DE=OD-DM=OM,
由①△OAD≌△BAE得,∠ODA=∠BEA=45°,
∴∠ODE=90°,
∵∠OAB=∠ODB=90°,∠OPA=∠BPD,
∴△OAP∽△BDP,
∴$\frac{OA}{AP}=\frac{BD}{PD}$,
∴$\frac{BC}{AP}=\frac{BD}{PD}$,
∵∠CBD=90°+∠ABE,∠APD=90°+∠AOD,
∠ABE=∠AOD,
∴∠CBD=∠APD,
∴△CBD∽△APD,
∴∠CDB=∠ADO=45°,
∴∠ODC=90°-45°=45°,
∵sin45°=$\frac{CF}{CD}$,
∴CF=$\frac{\sqrt{2}CD}{2}$,
∵△COF≌△OAM,
∴CF=OM,
∴BE-$\frac{1}{2}$DE=$\frac{\sqrt{2}}{2}$CD;
(3)如图3,∠KCG的大小不变,理由是:
过K作KM⊥AB于M,KN⊥BC,交CB的延长线于N,延长CG、BA交于Q,连接KQ,
∵∠N=∠MBN=∠BMK=90°,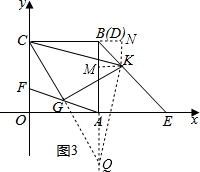
∴四边形BMKN是矩形,
∵AB=AE,∠BAE=90°,
∴∠ABE=45°,
∴BM=KM,
∴矩形BMKN是正方形,
∵OC∥AB,
∴∠OCG=∠GQA,
∵FG=AG,∠CGF=∠AGQ,
∴△FCG≌△AQG,
∴CG=QG,
∵CG⊥GK,
∴KC=KQ,
∵KN=KM,
∴Rt△CNK≌Rt△QMK,
∴∠CKN=∠QKM,
∴∠CKQ=∠CKM+∠MKQ=∠CKM+∠CKN=90°,
∴△KCQ是等腰直角三角形,
∴∠KCG=∠KQC=45°.
点评 本题是四边形的综合题,考查了正方形、等腰直角三角形、全等三角形的性质和判定;要注意以下两个问题:①对于第二问中的结论:和或差的形式,这是一个证明中的难点,要针对结论中出现的线段找对应的相等或倍数关系做替换,想办法把这些线段放在同一个三角形中或同一组相似或全等的图形中找关系,进行证明;②第三问中的角确定其定值还是范围,从这一角所在的三角形入手,找所有边存在的关系进行证明,得出结论.

| 气温(℃) | 11 | 13 | 14 | 15 | 16 |
| 天数(天) | 1 | 1 | 3 | 4 | 2 |
| A. | 三月下旬共有11天 | |
| B. | 三月下旬中,最低气温的众数是15℃ | |
| C. | 三月下旬中,最低气温的中位数是15℃ | |
| D. | 三月下旬中,最低气温的平均数是15℃ |
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数 | 4 | 8 | 12 | 11 | 5 |
| A. | 70分,80分 | B. | 80分,80分 | C. | 90分,80分 | D. | 80分,90分 |
 ,OD=3
,OD=3 ,求半圆O的半径长.
,求半圆O的半径长.
 ,
,  ,
,  ,求代数式
,求代数式 的值;
的值; -(a-b+c)
-(a-b+c)