题目内容
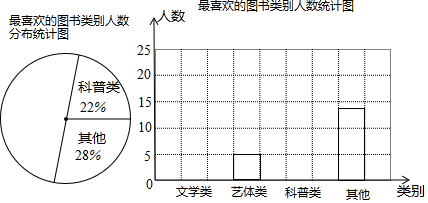
7.某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:学生最喜欢的图书类别人数统计表
| 图书类别 | 画记 | 人数 | 百分比 |
| 文学类 | |||
| 艺体类 | 正 | 5 | |
| 科普类 | 正正$\overline{\;}$ | 11 | 22% |
| 其他 | 正正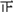 | 14 | 28% |
| 合计 | a | 100% |
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量a为50;
(2)补全扇形统计图和条形统计图;
(3)已知该校有600名学生,估计全校最喜欢文学类图书的学生有240人.
分析 (1)利用其他类的人数以及所占百分比,即可求出被调查的学生人数;
(2)利用(1)中所求得的总人数,根据各类别人数之和等于总人数求得文学类人数及其百分比,进而画出图形即可;
(3)用样本中文学类所占百分比乘以总人数可得答案.
解答 解:(1)随机抽取的样本容量a为14÷28%=50,
故答案为:50;
(2)文学类人数为50-(5+11+14)=20,其占总人数的百分比为$\frac{20}{50}$×100%=40%;
艺体类占总人数的百分比为$\frac{5}{50}$×100%=10%,
如图所示:
(3)估计全校最喜欢文学类图书的学生有600×40%=240(人),
故答案为:240.
点评 此题主要考查了条形统计图的应用以及扇形统计图应用、利用样本估计总体等知识,利用图形得出正确信息求出样本容量是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.下列各图中,∠1与∠2一定是互补关系的是( )
| A. |  | B. |  | C. |  | D. |  |
15.用代入法解方程组$\left\{\begin{array}{l}{2x-y=1①}\\{3y+4x=2②}\end{array}\right.$时,将①变形正确的是( )
| A. | y=2x+1 | B. | y=1-2x | C. | y=2x-1 | D. | y=-2x-1 |
19.一个多边形内角和的度数不可能的是( )
| A. | 180° | B. | 270° | C. | 360° | D. | 540° |
16. 如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
 如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )
如图,长方形ABCD中,沿折痕CE翻折△CDE得△CD′E,已知∠ECD′被BC分成的两个角相差15°,则图中∠1的度数为( )| A. | 35° | B. | 35°或50° | C. | 25°或70° | D. | 50°或70° |
 如图所示,将一块含30°角的直角三角板ABC绕点A旋转到三角形AED的位置,使得C、A、E三点在同一直线上,则旋转角是150度.
如图所示,将一块含30°角的直角三角板ABC绕点A旋转到三角形AED的位置,使得C、A、E三点在同一直线上,则旋转角是150度. 母亲节过后,永川区某校在本校学生中做了一次抽样调查,并把调查结果分成三种类型:A.已知道哪一天是母亲节的;B.知道但没有任何行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分),根据图中提供的信息,回答下列问题:
母亲节过后,永川区某校在本校学生中做了一次抽样调查,并把调查结果分成三种类型:A.已知道哪一天是母亲节的;B.知道但没有任何行动的;C.知道并问候母亲的.如图是根据调查结果绘制的统计图(部分),根据图中提供的信息,回答下列问题: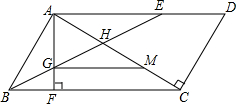 已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.
已知,在平行四边形ABCD中,E为AD上一点,且AB=AE,连接BE交AC于点H,过点A作AF⊥BC于F,交BE于点G.