题目内容
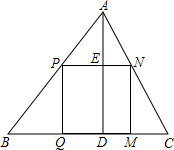
如图，△ABC是一块形状为三角形的余料，边BC=120cm，高AD=80cm，将其加工成矩形PQMN，使点Q、M在BC上，点P在AB上，点N在AC上，且PN：PQ=2：1，求PQ．
分析：根据四边形PQMN是矩形，得出PN∥QM∥BC，再利用比例式
=
，然后将PN：PQ=2：1，BC=120cm，高AD=80cm，分别代入即可求出PQ值．
| PN |
| BC |
| AE |
| AD |
解答：解：如图，
∵四边形PQMN是矩形，点Q、M在BC上，点P在AB上，点N在AC上，
∴PN∥QM∥BC，
又∵AD是高，
∴
=
，
而ED=PQ，
且PN：PQ=2：1，
∴
=
，
∴PQ=
=
=
（cm）．
∵四边形PQMN是矩形，点Q、M在BC上，点P在AB上，点N在AC上，
∴PN∥QM∥BC，
又∵AD是高，
∴
| PN |
| BC |
| AE |
| AD |
而ED=PQ，
且PN：PQ=2：1，
∴
| 2PQ |
| BC |
| AD-PQ |
| AD |
∴PQ=
| BC×AD |
| 2AD+BC |
=
| 120×80 |
| 2×80+120 |
=
| 240 |
| 7 |
点评：此题主要考查了矩形的对边平行且相等的性质，相似三角形对应高的比等于对应边的比的性质，数形结合找出相似三角形是解题的关键．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形一边在BC上，其余两个顶点分别在AB，AC上，那么这个正方形零件的边长应是
19、如图：△ABC是一块直角三角形余料，∠C=90度，工人师傅把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上，请你协助工人师傅用尺规画出裁割线．（不写画法，保留作图痕迹）
如图，△ABC是一块锐角三角形材料，边BC=6cm，高AD=4cm，要把它加工成一个矩形零件，使矩形的一边在BC上，其余两个顶点分别在AB、AC上，要使矩形EGFH的面积最大，EG的长应为
19、如图，△ABC是一块直角三角形余料，∠C=90°．工人师傅要把它加工成一个正方形零件，使C为正方形的一个顶点，其余三个顶点分别在AB、BC、AC边上．
如图，△ABC是一块锐角三角形材料，高线AH长8cm，底边BC长10cm，要把它加工成一个矩形零件，使矩形DEFG的一边EF在BC上，其余两个顶点D、G分别在AB、AC上，则四边形DEFG最大面积为（ ）cm2．