题目内容
12.解方程:(1)x2-6x=27
(2)4(x+2)2-81=0.
分析 (1)方程整理后,利用因式分解法求出解即可;
(2)方程变形后,利用平方根定义开方即可求出解.
解答 解:(1)方程整理得:x2-6x-27=0,即(x+3)(x-9)=0,
解得:x1=-3,x2=9;
(2)方程整理得:(x+2)2=$\frac{81}{4}$,
开方得:x+2=±$\frac{9}{2}$,
解得:x1=$\frac{5}{2}$,x2=-$\frac{13}{2}$.
点评 此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
4.对二次函数y=x2-2x-3,当y<0时,自变量x的取值范围是( )
| A. | -1<x<3 | B. | x<-1 | C. | x>3 | D. | x<-1或x>3 |
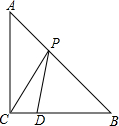 如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5.
如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5. 如图,已知点A、B、C、D在圆O上,AB=CD.
如图,已知点A、B、C、D在圆O上,AB=CD.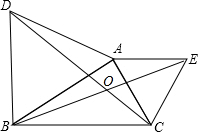 如图,△ABD和△AEC都是等边三角形;
如图,△ABD和△AEC都是等边三角形; 已知:如图,BC∥EF,AD=BE,BC=EF,求证:(1)△ABC≌△DEF.(2)AC∥DF.
已知:如图,BC∥EF,AD=BE,BC=EF,求证:(1)△ABC≌△DEF.(2)AC∥DF.