题目内容
12. 已知:如图,在△ABC中,∠A=90°,点D、E分别在AB、AC上,DE∥BC,CF与DE的延长线垂直,垂足为F.
已知:如图,在△ABC中,∠A=90°,点D、E分别在AB、AC上,DE∥BC,CF与DE的延长线垂直,垂足为F.(1)求证:∠B=∠ECF;
(2)若∠B=55°,求∠CED的度数.
分析 (1)先由DE∥BC得出∠B=∠ADE,再根据∠A=90°得出∠ADE+∠AED=90°.由∠F=90°可知∠ECF+∠CEF=90°.由对顶角相等可知∠AED=∠CEF,故∠ADE=∠ECF,由此可得出∠B=∠ECF;
(2)由(1)可知∠B=∠ECF=55°,故∠CED=∠F+∠ECF=90°+55°=145°.
解答 证明:(1)∵DE∥BC,
∴∠B=∠ADE.
∵∠A=90°,
∴∠ADE+∠AED=90°.
∵∠F=90°,
∴∠ECF+∠CEF=90°.
∵∠AED=∠CEF,
∴∠ADE=∠ECF,
∴∠B=∠ECF;
(2)∵由(1)可知∠B=∠ECF=55°,
∴∠CED=∠F+∠ECF=90°+55°=145°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
相关题目
3.方程3x2+5x+1=0的根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
2.下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第10个图形中白色正方形的个数为( )


| A. | 20 | B. | 30 | C. | 32 | D. | 34 |
 尺规作图:(要求保留作图痕迹,不要求写出作法)
尺规作图:(要求保留作图痕迹,不要求写出作法)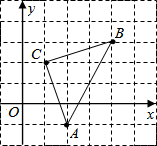 如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2). 已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E.求证:
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,作DE⊥AC于点E.求证: