题目内容
19.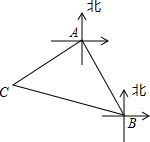 如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.
如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.
分析 由已知可得△ABC是等腰直角三角形,已知AB=10海里,根据等腰直角三角形的性质即可求得斜边BC的长.
解答 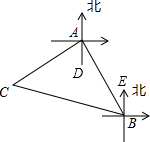 解:如图,由题意得,∠BAD=30°,∠CAD=60°,∠CBE=75°,AB=10海里.
解:如图,由题意得,∠BAD=30°,∠CAD=60°,∠CBE=75°,AB=10海里.
∵AD∥BE,
∴∠ABE=∠BAD=30°,
∴∠ABC=∠CBE-∠ABE=75°-30°=45°.
在△ABC中,∵∠BAC=∠BAD+∠CAD=30°+60°=90°,∠ABC=45°,
∴△ABC是等腰直角三角形,
∵AB=10海里,
∴BC=$\sqrt{2}$AB=10$\sqrt{2}$海里.
故答案为10$\sqrt{2}$.
点评 本题考查了解直角三角形的应用-方向角问题,等腰直角三角形的判定与性质,掌握方向角的定义从而证明△ABC是等腰直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,直线y=-1.5x+3上有一点P,则不等式-1.5x+3>1.5的解集是x<1.
如图,直线y=-1.5x+3上有一点P,则不等式-1.5x+3>1.5的解集是x<1.
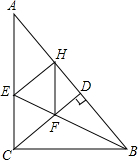 已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形.
已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形.