题目内容
9.解方程(1)x2-2x-2=0;
(2)(x-3)2+4x(x-3)=0.
(3)(x-3)(x+4)=8.
分析 (1)公式法求解可得;
(2)因式分解法求解可得;
(2)整理成一般式后,因式分解法求解可得.
解答 解:(1)∵a=1,b=-2,c=-2,
∴△=4-4×1×(-2)=12>0,
则x=$\frac{2±2\sqrt{3}}{2}$=1$±\sqrt{3}$;
(2)∵(x-3)(x-3+4x)=0,即(x-3)(5x-3)=0,
∴x-3=0或5x-3=0,
解得:x=3或x=$\frac{3}{5}$;
(3)整理成一般式为x2+x-20=0,
∵(x-4)(x+5)=0,
∴x-4=0或x+5=0,
解得:x=4或x=-5.
点评 本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

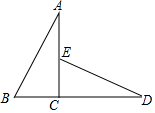 如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.
如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.