题目内容
2.已知二次函数y=-2x2+4x+1,当自变量取x1、x2时,函数值相等;当自变量取$\frac{{x}_{1}+{x}_{2}}{2}$时,函数值为3.分析 根据题意对称轴为x=$\frac{{x}_{1}+{x}_{2}}{2}$,把函数解析式化成顶点式y=-2(x-1)2+3,由顶点式求得对称轴x=1,顶点坐标为(1,3)即可求得自变量取$\frac{{x}_{1}+{x}_{2}}{2}$=1时,函数值为3.
解答 解:∵当自变量x取两个不同的值x1、x2时函数值相等,
∴对称轴为x=$\frac{{x}_{1}+{x}_{2}}{2}$,
∵y=-2x2+4x+1=-2(x-1)2+3,
∴对称轴x=1,顶点(1,3)
∴$\frac{{x}_{1}+{x}_{2}}{2}$=1,
∴当自变量取$\frac{{x}_{1}+{x}_{2}}{2}$=1时,函数值为3.
故答案为3.
点评 本题考查了二次函数图象上点的坐标特征,当自变量取x1、x2时,函数值相等,则对称轴为x=$\frac{{x}_{1}+{x}_{2}}{2}$是解题的关键.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
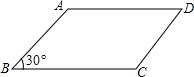 如图.已知?ABCD的周长为8cm,∠B=30°.若边长AB为xcm.写出?ABCD的面积y(cm2)与x(cm)的函数关系式.并求自变量x的取值范围.
如图.已知?ABCD的周长为8cm,∠B=30°.若边长AB为xcm.写出?ABCD的面积y(cm2)与x(cm)的函数关系式.并求自变量x的取值范围. 如图所示,已知等腰△ABC的一个内角是40°,且∠A=∠B,试求∠C的外角的度数.
如图所示,已知等腰△ABC的一个内角是40°,且∠A=∠B,试求∠C的外角的度数. 如图,已知CD∥AB∥MN,且EF∥BC,求证:AD∥EF.
如图,已知CD∥AB∥MN,且EF∥BC,求证:AD∥EF.