题目内容
8.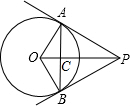 如图,点P为⊙O外一点,PA、PB分别与⊙O的相切于点A、B,线段AB、OP相交于点C,连接OA、OB,请写出两个你认为正确的结论(OA=OB除外):AP=BP,△AOP≌△BOP.
如图,点P为⊙O外一点,PA、PB分别与⊙O的相切于点A、B,线段AB、OP相交于点C,连接OA、OB,请写出两个你认为正确的结论(OA=OB除外):AP=BP,△AOP≌△BOP.
分析 已知PA、PB分别切⊙O于A、B,则满足切线的性质定理,以及切线长定理,可以得到AC与OP互相垂直,根据条件进一步可以得到相似三角形,全等三角形以及垂直关系.
解答 解:①AP=BP;
∵PA、PB分别与⊙O的相切于点A、B,
∴AP=BP
②△AOP≌△BOP;
在△AOP和△BOP中,
$\left\{\begin{array}{l}{OA=OB}\\{PA=PB}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△BOP;
还可以是OA2=OC•OP;AB⊥OP.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
18.宁波市轨道交通1号线一期工程批复总投资123.88亿元,其中123.88亿用科学记数法表示为( )
| A. | 123.88×108 | B. | 1.2388×1010 | C. | 1.2×1010 | D. | 0.12388×1011 |
 =0 D. x2﹣x+
=0 D. x2﹣x+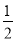 =0
=0
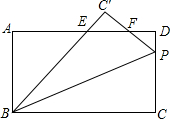 如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.
如图所示,矩形ABCD中,AB=6,BC=10,将矩形ABCD沿着过点B的直线折叠,使得点C落在点C′处,折痕所在直线与CD相交于点P,BC′与AD相交于点E,PC′与AD相交于点F,若△C′EF≌△DPF,则PC的长为$\frac{30}{7}$.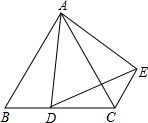 如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;
如图所示,△ABC是等边三角形,点D在BC上,△ABD经过逆时针方向旋转后到达△ACE的位置;