题目内容
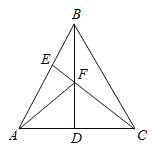
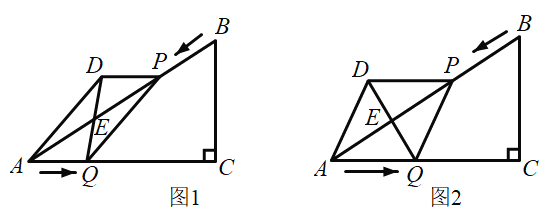
【题目】如图，在任意四边形
中，
，
，
，
分别是
，
，
，
上的点，对于四边形
的形状，某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ）
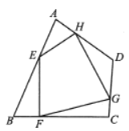
A.当，，，是各边中点，且
时，四边形为菱形
B.当，，，是各边中点，且
时，四边形为矩形
C.当，，，不是各边中点时，四边形可以为平行四边形
D.当，，，不是各边中点时，四边形不可能为菱形
【答案】D
【解析】
当E，F，G，H是四边形ABCD各边中点时，连接AC、BD，如图，根据三角形的中位线定理可得四边形EFGH是平行四边形，然后根据菱形的定义和矩形的定义即可对A、B两项进行判断；画出符合题意的平行四边形
，但满足
，
，
，
不是各边中点即可判断C项；画出符合题意的菱形，但满足，，，不是各边中点即可判断D项，进而可得答案．
解：A．当E，F，G，H是四边形ABCD各边中点时，连接AC、BD，如图，则由三角形的中位线定理可得：EH=
BD，EH∥BD；FG=BD，FG∥BD，所以EH=FG，EH∥FG，所以四边形EFGH是平行四边形；
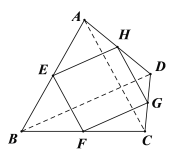
当AC＝BD时，∵EH=BD，EF=AC，∴EF=EH，故四边形EFGH为菱形，故A正确；
B．当E，F，G，H是四边形ABCD各边中点，且AC⊥BD时，如上图，由三角形的中位线定理可得：EH∥BD，EF∥AC，所以EH⊥EF，故平行四边形EFGH为矩形，故B正确；
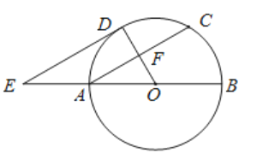
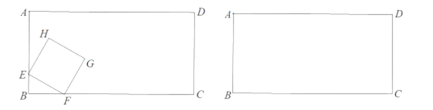
C．如图所示，若EF∥HG，EF＝HG，则四边形EFGH为平行四边形，此时E，F，G，H不是四边形ABCD各边中点，故C正确；
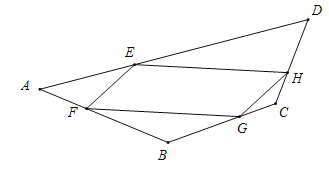
D．如图所示，若EF＝FG＝GH＝HE，则四边形EFGH为菱形，此时E，F，G，H不是四边形ABCD各边中点，故D错误；
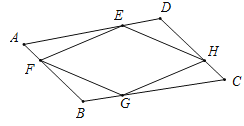
故选：D．
阅读快车系列答案
【题目】某大学生利用40天社会实践参与了某加盟店经营，他销售了一种成本为20元/件的商品，细心的他发现在第
天销售的相关数据可近似地用如下表中的函数表示：
销售量 | 销售单价 | |
| 当 | 当 |
（1）求前20天第几天获得的利润最大？最大利润是多少？
（2）求后20天第几天获得的利润最大？最大利润是多少？
（3）在后20天中，他决定每销售一件商品给山区孩子捐款
元（
且为整数），此时若还要求每一天的利润都不低于160元，求的值．
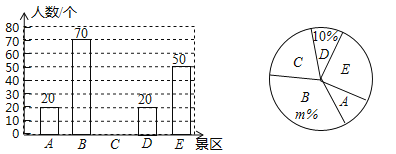
【题目】为了了解同学们每月零花钱的数额，校园小记者随机调查了本校部分同学，根据调查结果，绘制出了如下两个尚不完整的统计图表．
调查结果统计表
组别 | 分组（单位：元） | 人数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
调查结果扇形统计图
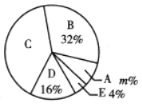
请根据以上图表，解答下列问题：
（1）这次被调查的同学共有______人，
________，
________；
（2）求扇形统计图中扇形
的圆心角度数；
（3）该校共有
人，请估计每月零花钱的数额
在
范围的人数．
