Question

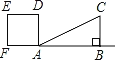
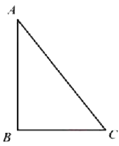
【题目】如图1所示，在中，，，．已知一点由点出发沿边向点匀速运动，点由点出发沿边向点匀速运动，两点的运动速度均为．以为邻边作平行四边形，连接，交边于点．假设两点运动的时间为(单位：)．

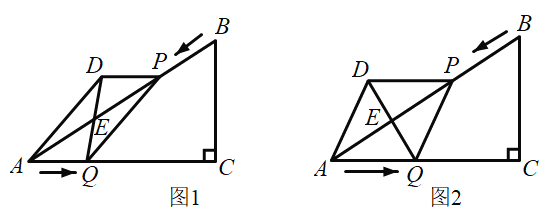
（1）求的长度；（用含有的代数式表示）

（2）当取何值时，平行四边形为矩形？

（3）如图2所示，当取何值时，？

Answer 1

【答案】（1）；（2）当时，平行四边形为矩形；（3）时，

【解析】

（1）由勾股定理求出AB=5dm，根据题意得AP=（5-t）dm，由平行四边形的性质可得AE；

（2）当平行四边形为矩形时，可证明∽，得，代入相关数据求解即可；

（3）当时，利用∠QAE与∠BAC的余弦值相等，列出方程式求解即可.

解：（1）在中，，．

由勾股定理可得

点由点出发沿边向点匀速运动，运动速度为

四边形为平行四边形

（2）当平行四边形为矩形时，，∥

∽，

即，解得

当时，平行四边形为矩形．

（3）当时，

则

即

解得

∴当时，．