题目内容
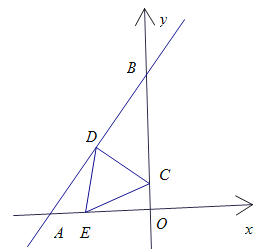
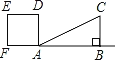
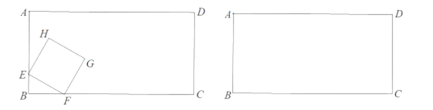
【题目】如图,在矩形![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 同时出发,点
同时出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,点
向终点匀速运动,点![]() 以每秒
以每秒![]() 个单位长度的速度沿边
个单位长度的速度沿边![]() 向终点匀速运动,以
向终点匀速运动,以![]() 为边在边
为边在边![]() 上方作正方形
上方作正方形![]() 设点
设点![]() 运动时间为
运动时间为![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)当点![]() 落在边
落在边![]() 上时,求此时
上时,求此时![]() 的值;
的值;
(3)设正方形![]() 与矩形
与矩形![]() 重叠图形的面积为
重叠图形的面积为![]() 请直接写出
请直接写出![]() 与
与![]() 之间的函数关系式,并写出
之间的函数关系式,并写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)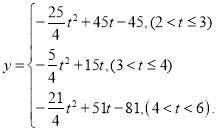
【解析】
(1)由题意可得BE,BF的长,由勾股定理即可求出EF;
(2)由四边形EFGH是正方形,易证得![]() ,进而得出
,进而得出![]() ,即可求得t的值;
,即可求得t的值;
(3)分![]() ,
,![]() ,
,![]() 三种情况进行分类讨论并画出图形,利用三角函数分别进行求解即可.
三种情况进行分类讨论并画出图形,利用三角函数分别进行求解即可.
(1) 由题意得,BE=t,BF=2t,
在Rt△BEF中,由勾股定理得,
![]() ,
,
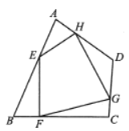
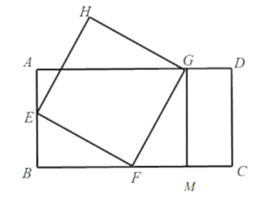
(2)当点![]() 落在边
落在边![]() 上时,如图所示,
上时,如图所示,
过点![]() 作
作![]() 于点
于点![]()
![]()
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
∵四边形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]()
![]()
![]()
在![]() 与
与![]() 中
中
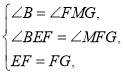
![]()
![]()
∵![]()
![]()
![]() ;
;
(3)①当![]() 时,如图,
时,如图,
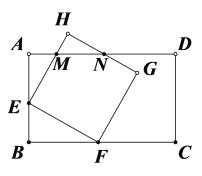
由题意得,BE=t,BF=2t,则AE=6-t,
∵四边形EFGH是正方形,
![]() ,
,
∴∠AEM+∠BEF=90°,∠BFE+∠BEF =90°,
∴∠BFE=∠AEM,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∵四边形ABCD是矩形,四边形EFGH是正方形,
∴∠EAM=∠MHN=90°,
∵∠AME=∠HMN,
∴∠AEM=∠HNM
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ;
;
②当![]() 时,过点M作MP⊥FG,如图,
时,过点M作MP⊥FG,如图,
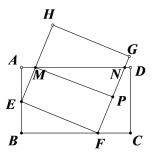
∵四边形EFGH是正方形,
∴∠HEF=∠GFE=90°,
∵MP⊥FG,
∴四边形MEFP是矩形,
∴∠EMP=90°,MP=EF=![]() ,
,
∴∠AME+∠PMN=90°,∠AEM+∠AME=90°,
∴∠AEM=∠PMN,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
③当![]() ,如图,
,如图,
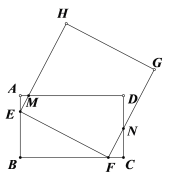
∵四边形EFGH是正方形,
∴∠EFG=90°,
∴∠BFE+∠NFC=90°,∠NFC+∠FNC =90°,
∴∠BFE =∠FNC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
综上所述,正方形![]() 与矩形
与矩形![]() 重叠图形的面积为:
重叠图形的面积为:
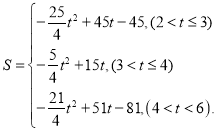

 名校课堂系列答案
名校课堂系列答案【题目】某商店计划一次性购进甲、乙两种商品共![]() 件,甲、乙两种商品的进价和售价如下表所示:
件,甲、乙两种商品的进价和售价如下表所示:
甲 | 乙 | |
进价(元/件) | 100 | 80 |
售价(元/件) | 150 | 120 |
设购进甲种商品的数量为![]() 件.
件.
(1)设进货成本为![]() 元,求
元,求![]() 与
与![]() 之间的函数解析式;若购进甲种商品的数量不少于
之间的函数解析式;若购进甲种商品的数量不少于![]() 件,则最低进货成本是多少元?
件,则最低进货成本是多少元?
(2)若除了进货成本,还要支付运费和销售员工工资共![]() 元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价
元,为尽快回笼资金,该商店决定对甲种商品进行降价销售,每件甲种商品降价![]() 元
元![]() ,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为
,乙种商品售价不变,设销售完甲、乙两种商品获得的总利润为![]() 元.
元.
①每件甲种商品的利润是 元(用含![]() 的代数式表示)
的代数式表示)
②求![]() 关于
关于![]() 的函数解析式
的函数解析式
③当![]() 时,请你根据
时,请你根据![]() 的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.
的取值范围,说明该商店购进甲种商品多少件时,获得的总利润最大.