题目内容
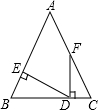 如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )
如图,已知△ABC中,∠B=∠C,D为BC上一点,FD⊥BC于D,ED⊥AB于E,∠AFD=150°,∠EDB的度数是( )| A、50° | B、40° |
| C、30° | D、60° |
考点:等腰三角形的性质
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C,即为∠B的度数,再根据直角三角形两锐角互余列式计算即可得解.
解答:解:∵FD⊥BC,
∴∠CDF=90°,
∴∠C=∠AFD-∠CDF=150°-90°=60°,
∴∠B=∠C=60°,
∵ED⊥AB,
∴∠BED=90°,
∴∠EDB=90°-∠B=90°-60°=30°.
故选C.
∴∠CDF=90°,
∴∠C=∠AFD-∠CDF=150°-90°=60°,
∴∠B=∠C=60°,
∵ED⊥AB,
∴∠BED=90°,
∴∠EDB=90°-∠B=90°-60°=30°.
故选C.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记各性质是解题的关键.

练习册系列答案
相关题目
在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
| A、5个 | B、10个 |
| C、15个 | D、45个 |
若关于x的方程2(
-k)x-3x=-1无解,则( )
| 1 |
| 2 |
| A、k=-1 | B、k=l |
| C、k≠-1 | D、k≠1 |
已知x=0是二次方程(m+1)x2+mx+4m2-4=0的一个解,那么m的值是( )
| A、0 | B、1 | C、-1 | D、±1 |
 如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有
如图,在△ABC中,∠ACB=90°,∠BAC=30°,在直线BC或AC上取一点P,使得△PAB为等腰三角形,这样的点P共有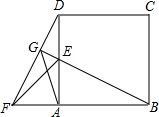 如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为
如图,在正方形ABCD的边BA的延长线上作等腰直角△AEF,连接DF,延长BE交DF于G.若FG=6,EG=2,则线段AG的长为 如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC.
如图:AD∥BC,AE平分∠BAD,CD与AE相交于M,且∠3=∠E,试说明:AB∥DC.